I welcome your thoughts on this post, but please read through to the end before commenting. Also, you’ll find the related code (in R) at the end. For those new to this blog, you may be taken aback (though hopefully not bored or shocked!) by how I expose my full process and reasoning. This is intentional and, I strongly believe, much more honest than presenting results without reference to how many different approaches were taken, or how many models were fit, before everything got tidied up into one neat, definitive finding.
Fast summaries
TL;DR (scientific version): Based solely on year-over-year changes in surface temperatures, the net increase since 1881 is fully explainable as a non-independent random walk with no trend.
TL;DR (simple version): Statistician does a test, fails to find evidence of global warming.
Introduction and definitions
As so often happens to terms which have entered the political debate, “global warming” has become infused with additional meanings and implications that go well beyond the literal statement: “the earth is getting warmer.” Anytime someone begins a discussion of global warming (henceforth GW) without a precise definition of what they mean, you should assume their thinking is muddled or their goal is to bamboozle. Here’s my own breakdown of GW into nine related claims:
- The earth has been getting warmer.
- This warming is part of a long term (secular) trend.
- Warming will be extreme enough to radically change the earth’s environment.
- The changes will be, on balance, highly negative.
- The most significant cause of this change is carbon emissions from human beings.
- Human beings have the ability to significantly reverse this trend.
- Massive, multilateral cuts to emissions are a realistic possibility.
- Such massive cuts are unlikely to cause unintended consequences more severe than the warming itself.
- Emissions cuts are better than alternative strategies, including technological fixes (i.e. iron fertilization), or waiting until scientific advances make better technological fixes likely.
Note that not all proponents of GW believe all nine of these assertions.
The data and the test (for GW1)
The only claims I’m going to evaluate are GW1 and GW2. For data, I’m using surface temperature information from NASA. I’m only considering the yearly average temperature, computed by finding the average of four seasons as listed in the data. The first full year of (seasonal) data is 1881, the last year is 2011 (for this data, years begin in December and end in November).
According to NASA’s data, in 1881 the average yearly surface temperature was 13.76°C. Last year the same average was 14.52°C, or 0.76°C higher (standard deviation on the yearly changes is 0.11°C). None of the most recent ten years have been colder than any of the first ten years. Taking the data at face value (i.e. ignoring claims that it hasn’t been properly adjusted for urban heat islands or that it has been manipulated), the evidence for GW1 is indisputable: The earth has been getting warmer.
Usually, though, what people mean by GW is more than just GW; they mean GW2 as well, since without GW2 none of the other claims are tenable, and the entire discussion might be reduced to a conversation like this:
“I looked up the temperature record this afternoon, and noticed that the earth is now three quarters of a degree warmer than it was in the time of my great great great grandfather.”
“Why, I do believe you are correct, and wasn’t he the one who assassinated James A. Garfield?”
“No, no, no. He’s the one who forced Sitting Bull to surrender in Saskatchewan.”
Testing GW2
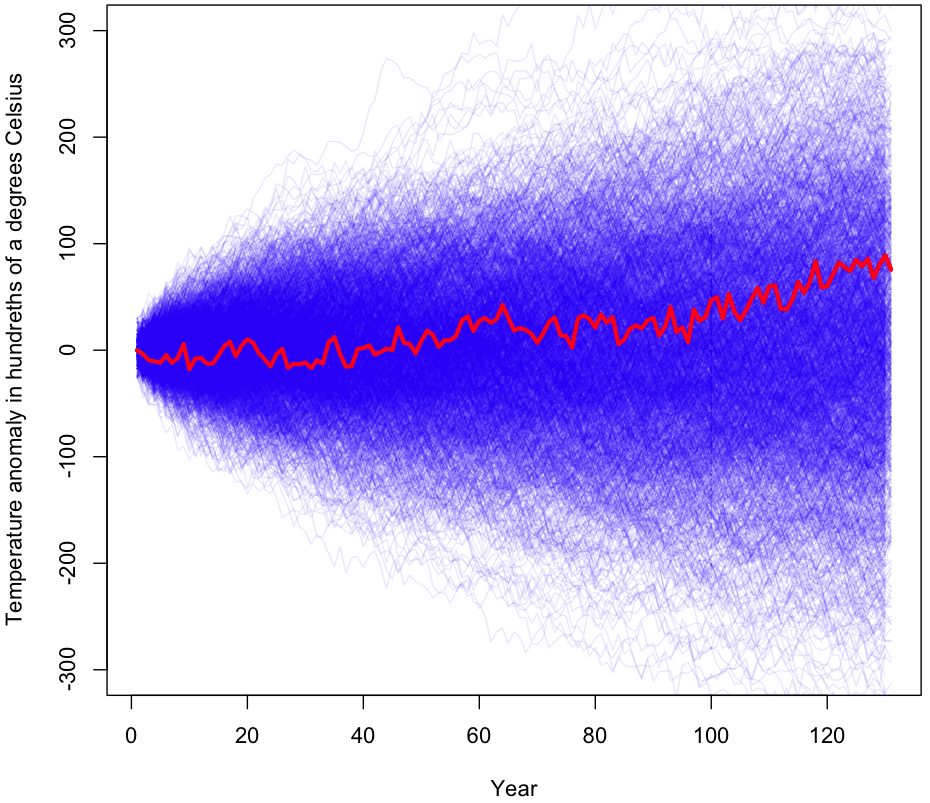
Do the data compel us to view GW as part of a trend and not just background noise? To evaluate this claim, I’ll be taking a standard hypothesis testing approach, starting with the null hypothesis that year-over-year (YoY) temperature changes represent an undirected random walk. Under this hypothesis, the YoY changes are modeled as a independent draws from a distribution with mean zero. The final temperature represents the sum of 130 of these YoY changes. To obtain my sampling distribution, I’ve calculated the 130 YoY changes in the data, then subtracted the mean from each one. This way, I’m left with a distribution with the same variance as in the original data. YoY jumps in temperature will be just as spread apart as before, but with the whole distribution shifted over until its expected value becomes zero. Note that I’m not assuming a theoretical distributional form (eg Normality), all of the data I’m working with is empirical.
My test will be to see if, by sampling 130 times (with replacement!) from this distribution of mean zero, we can nonetheless replicate a net change in global temperatures that’s just as extreme as the one in the original data. Specifically, our p-value will be the fraction of times our Monte Carlo simulation yields a temperature change of greater than 0.76°C or less than -0.76°C. Note that mathematically, this is the same test as drawing from the original data, unaltered, then checking how often the sum of changes resulted in a net temperature change of less than 0 or more than 1.52°C.
I have not set a “critical” p-value in advance for rejecting the null hypothesis, as I find this approach to be severely limiting and just as damaging to science as J-Lo is to film. Instead, I’ll comment on the implied strength of the evidence in qualitative terms.
Initial results
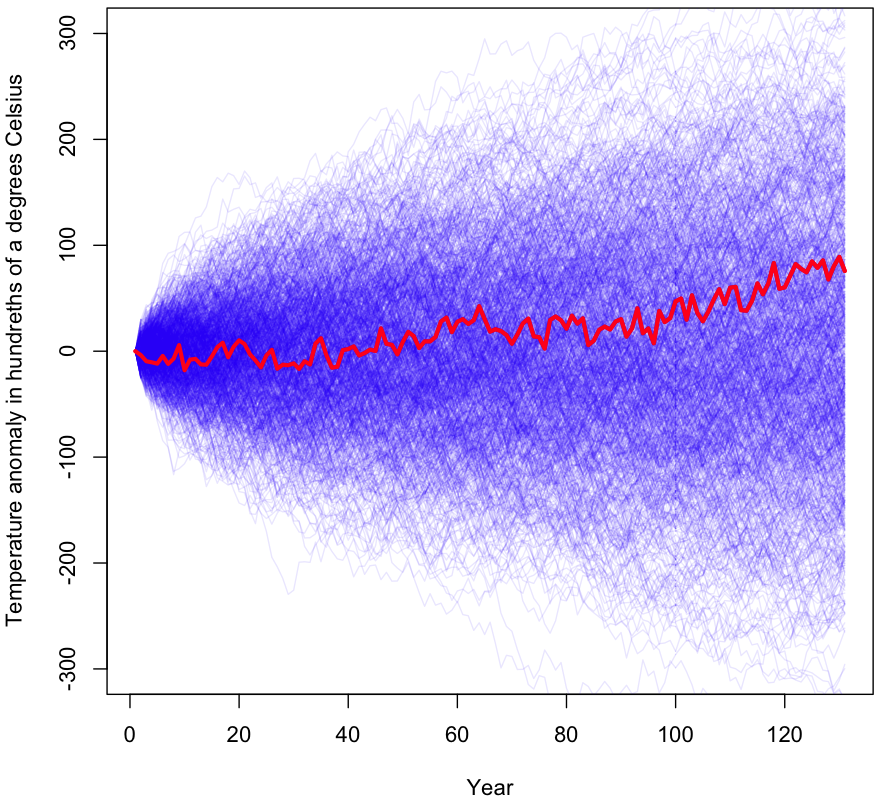
The initial results are shown graphically at the beginning of this post (I’ll wait while you scroll back up). As you can see, a large percentage of the samples gave a more extreme temperature change than what was actually observed (shown in red). During the 1000 trials visualized, 56% of the time the results were more extreme than the original data after 130 years worth of changes. I ran the simulation again with millions of trials (turn off plotting if you’re going to try this!); the true p-value for this experiment is approximately 0.55.
For those unfamiliar with how p-values work, this means that, assuming temperature changes are randomly plucked out of a bundle of numbers centered at zero (ie no trend exists), we would still see equally dramatic changes in temperature 55% of the time. Under even the most generous interpretation of the p-value, we have no reason to reject the null hypothesis. In other words, this test finds zero evidence of a global warming trend.
Testing assumptions Part 1
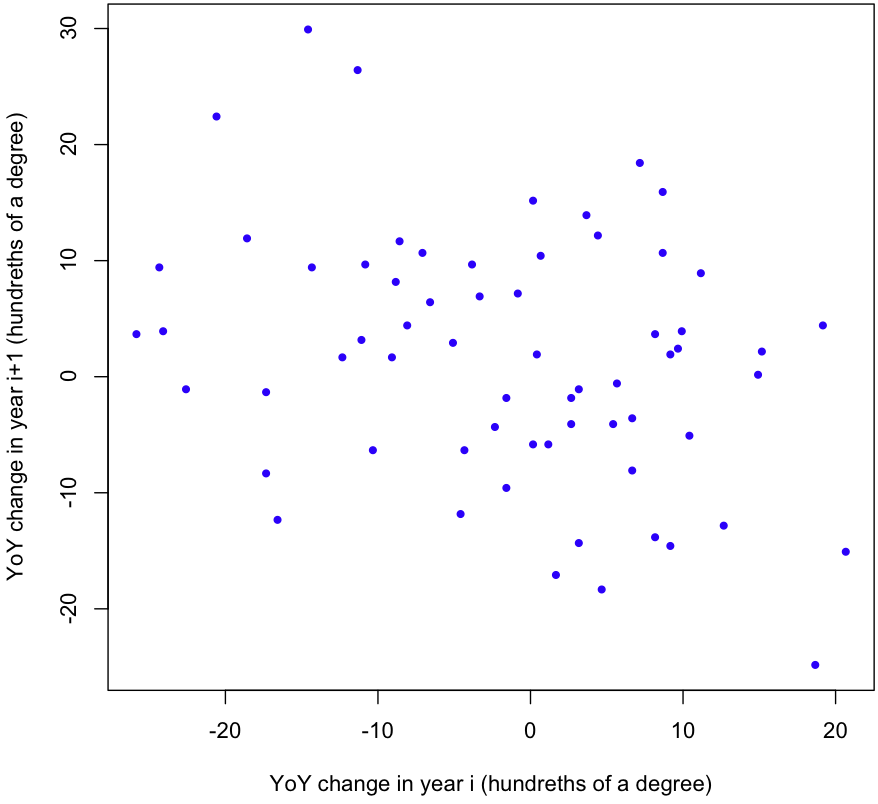
But wait! We still haven’t tested our assumptions. First, are the YoY changes independent? Here’s a scatterplot showing the change in temperature one year versus the change in temperature the next year:
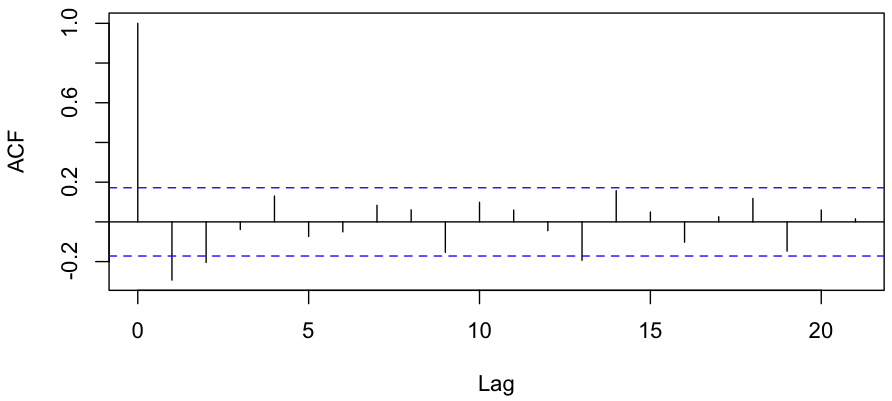
Looks like there’s a negative correlation. A quick linear regression gives a p-value of 0.00846; it’s highly unlikely that the correlation we see (-0.32) is mere chance. One more test worth running is the ACF, or the Autocorrelation function. Here’s the plot R gives us:
Evidence for a negative correlation between consecutive YoY changes is very strong, and there’s some evidence for a negative correlation between YoY changes which are 2 years apart as well.
Before I explain how to incorporate this information into a revised Monte Carlo simulation, what does a negative correlation mean in this context? It tells us that if the earth’s temperature rises by more than average in one year, it’s likely to fall (or rise less than average) the following year, and vice versa. The bigger the jump one way, the larger the jump the other way next year (note this is not a case of regression to the mean; these are changes in temperature, not absolute temperatures. Update: This interpretation depends on your assumptions. Specifically, if you begin by assuming a trend exists, you could see this as regression to the mean. Note, however, that if you start with noise, then draw a moving average, this will induce regression to the mean along your “trendline”). If anything, this is evidence that the earth has some kind of built in balancing mechanism for global temperature changes, but as a non-climatologist all I can say is that the data are compatible with such a mechanism; I have no idea if this makes sense physically.
Correcting for correlation
What effect will factoring in this negative correlation have on our simulation? My initial guess is that it will cause the total temperature change after 130 years to be much smaller than under the pure random walk model, since changes one year are likely to be balanced out by changes next year in the opposite direction. This would, in turn, suggest that the observed 0.76°C change over the past 130 years is much less likely to happen without a trend.
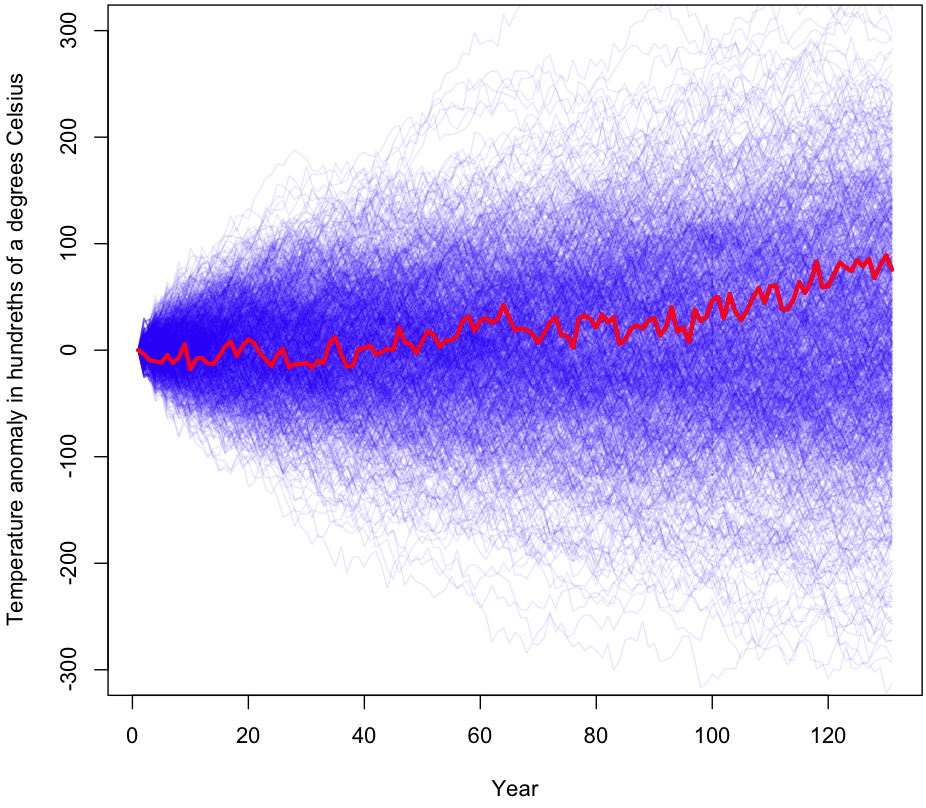
The most straightforward way to incorporate this correlation into our simulation is to sample YoY changes in 2-year increments. Instead of 130 individual changes, we take 65 changes from our set of centered changes, then for each sample we look at that year’s changes and the year that immediately follows it. Here’s what the plot looks like for 1000 trials.
After doing 100,000 trials with 2 year increments, we get a p-value of 0.48. Not much change, and still far from being significant. Sampling 3 years at a time brings our p-value down to 0.39. Note that as we grab longer and longer consecutive chains at once, the p-value has to approach 0 (asymptotically) because we are more and more likely to end up with the original 130 year sequence of (centered) changes, or a sequence which is very similar. For example, increasing our chain from one YoY change to three reduces the number of samplings from 130130 to approximately 4343 – still a huge number, but many orders of magnitude less (Fun problem: calculate exactly how many fewer orders of magnitude. Hint: If it takes you more than a few minutes, you’re doing it wrong).
Correcting for correlation Part 2 (A better way?)
To be more certain of the results, I ran the simulation in a second way. First I sampled 130 of the changes at random, then I threw out any samplings where the correlation coefficient was greater than -0.32. This left me with the subset of random samplings whose coefficients were less than -0.32. I then tested these samplings to see the fraction that gave results as extreme as our original data.
Compared to the chained approach above, I consider this to be a more “honest” way to sample an empirical distribution, given the constraint of a (maximum) correlation threshold. I base this on E.T. Jaynes’ demonstration that, in the face of ignorance as to how a particular statistic was generated, the best approach is to maximize the (informational) entropy. The resulting solution is the most likely result you would get if you sampled from the full space (uniformly), then limited your results to those which match your criteria. Intuitively, this approach says: Of all the ways to arrive at a correlation of -0.32 or less, which are the most likely to occur?
For a more thorough discussion of maximum entropy approaches, see Chapter 11 of Jaynes’ book “Probability Theory” or his “Papers on Probability” (1979). Note that this is complicated, mind-blowing stuff (it was for me, anyway). I strongly recommend taking the time to understand it, but don’t bother unless you have at least an intermediate-level understanding of math and probability.
Here’s what the plot looks like subject to the correlation constraint:
If it looks similar to the other plots in terms of results, that’s because it is. Empirical p-value from 1000 trials? 0.55. Because generating samples with the required correlation coefficients took so long, these were the only trials I performed. However, the results after 1000 trials are very similar to those for 100,000 or a million trials, and with a p-value this high there’s no realistic chance of getting a statistically significant result with more trials (though feel free to try for yourself using the R code and your cluster of computers running Hadoop). In sum, the maximum entropy approach, just like the naive random walk simulation and the consecutive-year simulations, gives us no reason to doubt our default explanation of GW2 – that it is the result of random, undirected changes over time.
One more assumption to test
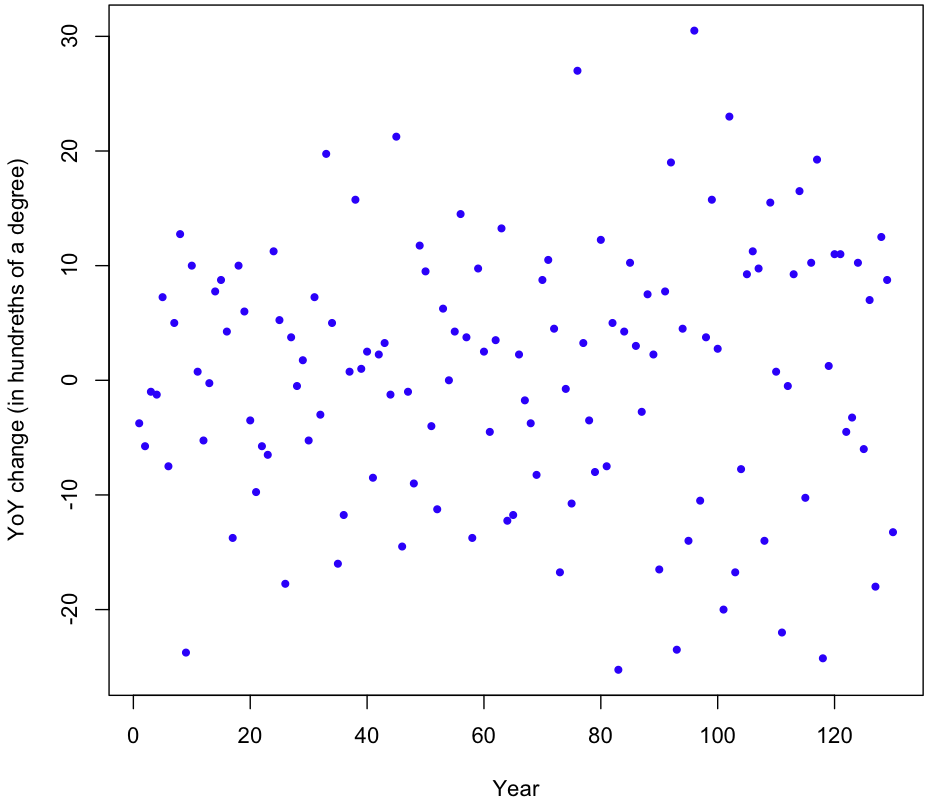
Another assumption in our model is that that YoY changes have constant variance over time (homoscedasticity). Here’s the plot of the (raw, uncentered) YoY changes:
It appears that the variance might be increasing over time, but just looking at the plot isn’t conclusive. To be sure, I took the absolute value of the changes and ran a simple regression on them. The result? Variance is increasing (p-value 0.00267), though at a rate that’s barely perceptible; the estimated absolute increase in magnitude of the YoY changes is 0.046. That figure is in hundreths of degrees Celsius, so our linear model gives a rate of increase in variability of just 4.6 ten-thousands of a degree per year. Over the course of 130 years, that equates to an increase of six hundredths of a degree Celsius (margin of error of 3.9 hundredths at two std deviations). This strikes me as a miniscule amount, though relative to the size of the YoY changes themselves it’s non-trivial.
Does this increase in volatility invalidate our simulation? I don’t think so. Any model which took into account this increase in volatility (while still being centered) would be more likely to produce extreme results under the null hypothesis of undirected change. In other words, the bigger the yearly temperature changes, the more likely a random sampling of those changes will lead us far away from our 13.8°C starting point in 1881, with most of the variation coming towards the end. If we look at the data, this is exactly what happens. During the first 63 years of data the temperature increases by 42 hundredths of a degree, then drops 40 hundredths in just 12 years, then rises 80 hundredths within 25 years of that; the temperature roller coaster is becoming more extreme over time, as variability increases.
Beyond falsifiability
Philosopher Karl Popper insisted that for a theory to be scientific, it must be falsifiabile. That is, there must exist the possibility of evidence to refute the theory, if the theory is incorrect. But falsifiability, by itself, is too low a bar for a theory to gain acceptance. Popper argued that there were gradations and that “the amount of empirical information conveyed by a theory, or it’s empirical content, increases with its degree of falsifiability” (emphasis in original).
Put in my words, the easier it is to disprove a theory, the more valuable the theory. (Incorrect) theories are easy to disprove if they give narrow prediction bands, are testable in a reasonable amount of time using current technology and measurement tools, and if they predict something novel or unexpected (given our existing theories).
Perhaps you have already begun to evaluate the GW claims in terms of these criteria. I won’t do a full assay of how the GW theories measure up, but I will note that we’ve had several long periods (10 years or more) with no increase in global temperatures, so any theory of GW3 or GW5 will have to be broad enough to encompass decades of non-warming, which in turn makes the theory much harder to disprove. We are in one of those sideways periods right now. That may be ending, but if it doesn’t, how many more years of non-warming would we need for scientists to abandon the theory?
I should point out that a poor or a weak theory isn’t the same as an incorrect theory. It’s conceivable that the earth is in a long-term warming trend (GW2) and that this warming has a man-made component (GW5), but that this will be a slow process with plenty of backsliding, visible only over hundreds or thousands of years. The problem we face is that GW3 and beyond are extreme claims, often made to bolster support for extreme changes in how we live. Does it make sense to base extreme claims on difficult to falsify theories backed up by evidence as weak as the global temperature data?
Invoking Pascal’s Wager
Many of the arguments in favor of radical changes to how we live go like this: Even if the case for extreme man-made temperature change is weak, the consequences could be catastrophic. Therefore, it’s worth spending a huge amount of money to head off a potential disaster. In this form, the argument reminds me of Pascal’s Wager, named after Blaise Pascal, a 17th century mathematician and co-founder of modern probability theory. Pascal argued that you should “wager” in favor of the existance of God and live life accordingly: If you are right, the outcome is infinitely good, whereas if you are wrong and there is no God, the most you will have lost is a lifetime of pleasure.
Before writing this post, I Googled to see if others had made this same connection. I found many discussions of the similarities, including this excellent article by Jim Manzi at The American Scene. Manzi points out problems with applying Pascal’s Wager, including the difficulty in defining a stopping point for spending resources to prevent the event. If a 20°C increase in temperature is possible, and given that such an increase would be devastating to billions of people, then we should be willing to spend a nearly unlimited amount to avert even a tiny chance of such an increase. The math works like this: Amount we should be willing to spend = probability of 20°C increase (say 0.00001) * harm such an increase would do (a godzilla dollars). The end result is bigger than the GDP of the planet.
Of course, catastrophic GW isn’t the only potential threat can have Pascal’s Wager applied to it. We also face annihilation from asteroids, nuclear war, and new diseases. Which of these holds the trump card to claim all of our resources? Obviously we need some other approach besides throwing all our money at the problem with the scariest Black Swan potential.
There’s another problem with using Pascal’s Wager style arguments, one I rarely see discussed: proponents fail to consider the possibility that, in radically altering how we live, we might invite some other Black Swan to the table. In his original argument, Pascal the Jansenist (sub-sect of Christianity) doesn’t take into account the possibility that God is a Muslim and would be more upset by Pascal’s professed Christianity than He would be with someone who led a secular lifestyle. Note that these two probabilities – that God is Muslim who hates Christians more than atheists, or that God is Christian and hates atheists – are incommesurable! There’s no rational way to weigh them and pick the safer bet.
What possible Black Swans do we invite by forcing people to live at the same per-capita energy-consumption level as our forefathers in the time of James A. Garfield?
Before moving on, I should make clear that humans should, in general, be very wary of inviting Black Swans to visit. This goes for all experimentation we do at the sub-atomic level, including work done at the LHC (sorry!), and for our attempts to contact aliens (as Stephen Hawking has pointed out, there’s no certainty that the creatures we attract will have our best interests in mind). So, unless we can point to strong, clear, tangible benefits from these activities, they should be stopped immediately.
Beware the anthropic principle
Strictly speaking, the anthropic principle states that no matter how low the odds are that any given planet will house complex organisms, one can’t conclude that the existence of life on our planet is a miracle. Essentially, if we didn’t exist, we wouldn’t be around to “notice” the lack of life. The chance that we should happen to live on a planet with complex organisms is 1, because it has to be.
More broadly, the anthropic principle is related to our tendency to notice extreme results, then assume these extremes must indicate something more than the noise inherent in random variation. For example, if we gathered together 1000 monkeys to predict coin tosses, it’s likely that one of them will predict the first 10 flips correctly. Is this one a genius, a psychic, an uber-monkey? No. We just noticed that one monkey because its record stood out.
Here’s another, potentially lucrative, most likely illegal, definitely immoral use of the anthropic principle. Send out a million email messages. In half of them, predict that a particular stock will go up the next day, in the other half predict it will go down. The next day, send another round of predictions to just those emails that got the correct prediction the first time. Continue sending predictions to only those recipients who receive the correct guesses. After a dozen days, you’ll have a list of people who’ve seen you make 12 straight correct predictions. Tell these people to buy a stock you want to pump and dump. Chances are good they’ll bite, since from their perspective you look like a stock-picking genius.
What does this have to do with GW? It means that we have to disentangle our natural tendency to latch on to apparent patterns from the possibility that this particular pattern is real, and not just an artifact of our bias towards noticing unlikely events under null hypotheses.
Biases, ignorance, and the brief life, death, and afterlife of a pet theory
While the increase in volatility seen in the temperature data complicates our analysis of the data, it gives me hope for a pet theory about climate change which I’d buried last year (where does one bury a pet theory?). The theory (for which I share credit with my wife and several glasses of wine) is that the true change in our climate should best be described as Distributed Season Shifting, or DSS. In short, DSS states that we are now more likely to have unseasonably warm days during the colder months, and unseasonably cold days during the warmer months. Our seasons are shifting, but in a chaotic, distributed way. We built this theory after noticing a “weirdening” of our weather here in Toronto. Unfortunately (for the theory), no matter how badly I tortured the local temperature data, I couldn’t get it to confess to DSS.
However, maybe I was looking at too small a sample of data. The observed increase in volatility of global YoY changes might also be reflected in higher volatility within the year, but the effects may be so small that no single town’s data is enough to overcome the high level of “normal” volatility within seasonal weather patterns.
My tendency to look for confirmation of DSS in weather data is a bias. Do I have any other biases when it comes to GW? If anything, as the owner of a recreational property located north of our northern city, I have a vested interest in a warmer earth. Both personally (hotter weather = more swimming) and financially, GW2 and 3 would be beneficial. In a Machiavellian sense, this might give me an incentive to downplay GW2 and beyond, with the hope that our failure to act now will make GW3 inevitable. On the other hand, I also have an incentive to increase the perception of GW2, since I will someday be selling my place to a buyer who will base her bid on how many months of summer fun she expects to have in years to come.
Whatever impact my property ownership and failed theory have on this data analysis, I am blissfully free of one biasing factor shared by all working climatologists: the pressures to conform to peer consensus. Don’t underestimate the power of this force! It effects everything from what gets published to who gets tenure. While in the long run scientific evidence wins out, the short run isn’t always so short: For several decades the medical establishment pushed the health benefits of a low fat, high carb diet. Alternative views are only now getting attention, despite hundreds of millions of dollars spent on research which failed to back up the consensus claims.
Is the overall evidence for GW2 – 9 as weak as the evidence used to promote high carb diets? I have no idea. Beyond the global data I’m examining here, and my failed attempt to “discover” DSS in Toronto’s temperature data, I’m coming from a position of nearly complete ignorance: I haven’t read the journal articles, I don’t understand the chemistry, and I’ve never seen Al Gore’s movie.
Final analysis and caveats
Chances are, if you already had strong opinions about the nine faces of GW before reading this article, you won’t have changed your opinion much. In particular, if a deep understanding of the science has convinced you that GW is a long term, man-made trend, you can point out that I haven’t disproven your view. You could also argue the limitations of testing the data using the data, though I find this more defensible than testing the data with a model created to fit the data.
Regardless of your prior thinking, I hope you recognize that my analysis shows that YoY temperature data, by itself, provides no evidence for GW2 and beyond. Also, because of the relatively long periods of non-warming within the context of an overall rise in global temperature, any correct theory of GW must include backsliding within it’s confidence intervals for predictions, making it a weaker theory.
What did my analysis show for sure? Clearly, temperatures have risen since the 1880s. Also, volatility in temperature changes has increased. That, of itself, has huge implications for our lives, and tempts me to do more research on DSS (what do you call pet theory that’s risen from the dead?). I’ve also become intrigued with the idea that our climate (at large) has mechanisms to balance out changes in temperature. In terms of GW2 itself, my analysis has not convinced me that it’s all a myth. If we label random variation “noise” and call trend a “signal,” I’ve shown that yearly temperature changes are compatible with an explanation of pure noise. I haven’t shown that no signal exists.
Thanks for reading all the way through! Here’s the code:
Code in R
theData = read.table("/path/to/theData/FromNASA/cleanedForR.txt", header=T)
# There has to be a more elegant way to do this
theData$means = rowMeans(aggregate(theData[,c("DJF","MAM","JJA","SON")], by=list(theData$Year), FUN="mean")[,2:5])
# Get a single vector of Year over Year changes
rawChanges = diff(theData$means, 1)
# SD on yearly changes
sd(rawChanges)
# Subtract off the mean, so that the distribution now has an expectaion of zero
changes = rawChanges - mean(rawChanges)
# Find the total range, 1881 to 2011
(theData$means[131] - theData$means[1])/100
# Year 1 average, year 131 average, difference between them in hundreths
y1a = theData$means[1]/100 + 14
y131a = theData$means[131]/100 + 14
netChange = (y131a - y1a)*100
# First simulation, with plotting
plot.ts(cumsum(c(0,rawChanges)), col="red", ylim=c(-300,300), lwd=3, xlab="Year", ylab="Temperature anomaly in hundreths of a degrees Celsius")
trials = 1000
finalResults = rep(0,trials)
for(i in 1:trials) {
jumps = sample(changes, 130, replace=T)
# Add lines to plot for this, note the "alpha" term for transparency
lines(cumsum(c(0,jumps)), col=rgb(0, 0, 1, alpha = .1))
finalResults[i] = sum(jumps)
}
# Re-plot red line again on top, so it's visible again
lines(cumsum(c(0,rawChanges)), col="red", ylim=c(-300,300), lwd=3)
# Fnd the fraction of trials that were more extreme than the original data
( length(finalResults[finalResults>netChange]) + length(finalResults[finalResults<(-netChange)]) ) / trials # Many more simulations, minus plotting trials = 10^6 finalResults = rep(0,trials) for(i in 1:trials) { jumps = sample(changes, 130, replace=T) finalResults[i] = sum(jumps) } # Fnd the fraction of trials that were more extreme than the original data ( length(finalResults[finalResults>netChange]) + length(finalResults[finalResults<(-netChange)]) ) / trials # Looking at the correlation between YoY changes x = changes[seq(1,129,2)] y = changes[seq(2,130,2)] plot(x,y,col="blue", pch=20, xlab="YoY change in year i (hundreths of a degree)", ylab="YoY change in year i+1 (hundreths of a degree)") summary(lm(x~y)) cor(x,y) acf(changes) # Try sampling in 2-year increments plot.ts(cumsum(c(0,rawChanges)), col="red", ylim=c(-300,300), lwd=3, xlab="Year", ylab="Temperature anomaly in hundreths of a degrees Celsius") trials = 1000 finalResults = rep(0,trials) for(i in 1:trials) { indexes = sample(1:129,65,replace=T) # Interlace consecutive years, to maintian the order of the jumps jumps = as.vector(rbind(changes[indexes],changes[(indexes+1)])) lines(cumsum(c(0,jumps)), col=rgb(0, 0, 1, alpha = .1)) finalResults[i] = sum(jumps) } # Re-plot red line again on top, so it's visible again lines(cumsum(c(0,rawChanges)), col="red", ylim=c(-300,300), lwd=3) # Find the fraction of trials that were more extreme than the original data ( length(finalResults[finalResults>netChange]) + length(finalResults[finalResults<(-netChange)]) ) / trials # Try sampling in 3-year increments trials = 100000 finalResults = rep(0,trials) for(i in 1:trials) { indexes = sample(1:128,43,replace=T) # Interlace consecutive years, to maintian the order of the jumps jumps = as.vector(rbind(changes[indexes],changes[(indexes+1)],changes[(indexes+2)])) # Grab one final YoY change to fill out the 130 jumps = c(jumps, sample(changes, 1)) finalResults[i] = sum(jumps) } # Fnd the fraction of trials that were more extreme than the original data ( length(finalResults[finalResults>netChange]) + length(finalResults[finalResults<(-netChange)]) ) / trials # The maxEnt method for conditional sampling lines(cumsum(c(0,rawChanges)), col="red", ylim=c(-300,300), lwd=3) trials = 1000 finalResults = rep(0,trials) for(i in 1:trials) { theCor = 0 while(theCor > -.32) {
jumps = sample(changes, 130, replace=T)
theCor = cor(jumps[1:129],jumps[2:130])
}
# Add lines to plot for this
lines(cumsum(jumps), col=rgb(0, 0, 1, alpha = .1))
finalResults[i] = sum(jumps)
}
# Re-plot red line again on top, so it's visible again
lines(cumsum(c(0,rawChanges)), col="red", ylim=c(-300,300), lwd=3)
( length(finalResults[finalResults>74]) + length(finalResults[finalResults<(-74)]) ) / trials
# Plot of YoY changes over time
plot(rawChanges,pch=20,col="blue", xlab="Year", ylab="YoY change (in hundreths of a degree)")
# Is there a trend?
absRawChanges = abs(rawChanges)
pts = 1:130
summary(lm(absRawChanges~pts))
Tags: global warming, NASA, pascal's wager

Very good piece. Do you see the variance/time it is lower at end.
Hi,
Thanks for the making the code available. Could you maybe expand on the idea that the correlation between YoY is not regression to the mean?
In random data, you see a negative correlation for the YoY change.
x <- rnorm(1000)
dx <- diff(x)
plot(dx[-length(dx)], dx[-1])
cor.test(dx[-length(dx)], dx[-1])
Thanks,
G
Sure Gio. For those who don’t know what we’re talking about, “regression to the mean” is the tendency for extreme deviations from the model to be followed by less extreme deviations. To return to the example of the monkeys flipping coins: The better a monkey does during its first 10 predictions, the more likely it is to do worse (closer to the mean of 0.5) on its next 10. Likewise, a very unlucky monkey will probably “improve” its prediction powers on the next 10 guesses as it “regresses to the mean” of 0.5. Shameless plug: I slipped in a reference to regression to the mean in my comic (that page isn’t shown in the samples).
This (my analysis) is not a case of regression to the mean because the mean changes each time to be the previous year’s temperature, and we are examining all the monkeys. For example, if you create the following random walk:
x = rnorm(1000)
y = cumsum(x)
plot.ts(y, col=”blue”)
Then your YoY changes are the (IID) x’s, and hence uncorrelated. Try:
cor(x[1:999],x[2:1000])
or
cor(x[seq(1,999,2)],x[seq(2,1000,2)])
and you should get a very low observed correlation coefficient.
EDIT: I should clarify that if we JUST looked at the most extreme individual YoY changes, then these would be likely to be followed by a less extreme change. However, we’re looking at the full emperical distribution of YoY changes.
@J. Li:
Do you mean that variance begins to go back down in the final years? I’ll look into that.
Great post.
Thanks! I have been trying to explian some of this to my son and this post is awesome! Richard Feynman had some great discussions on the concept that we lend too much credence to a theory and then alter the results to match – basically throwing away any data that does not match our theory as an outlier and thereby decreasing knowledge because we skew the model. It has been difficult to get past the political and financial stress on this topic so I appreciate your appeal to statistics.
Thom … I appreciate your reference to Richard Feynman!
Here’s what you’ve done:
1) Construct a straw man argument for anthropogenic global warming.
2) Admit that you know essentially nothing about climate science or about the arguments that actual people have put forth for AGW.
3) Discover that your straw man argument fails (surprise!)
4) Slap a provocative title on your post and call it a day.
If you were a journalist or an academic this would be negligent. As a blogger, I guess it’s a good strategy because it got you some page views.
Hi Mike,
What “straw man” are you referring to? Unless you consider the global temperature data itself to be orthogonal to the theory of anthropogenic GW, analyzing its strength is relevant.
I believe the “straw man” here is that global temperatures should not follow a random walk in the event of GW2. The problem with this standard is that the random walk is not a valid model of the earth’s climate. Here’s a post featuring a debate between statisticians and physical scientists on exactly this topic. I’m certain by even superficially consulting an expert you could find further work in this area, but if you fear for your own ability to stand up in the face of “peer concensus” I advice against reading any topical work on the matter.
On the question of peer concensus, the tools of science (which you happily disregard) are specifically designed to combat this type of groupthink. While you’re right there are cases where it has failed, the number of successes attributable to the scientific method are too numerous to name.
Failed to attach link mentioned above.
http://ourchangingclimate.wordpress.com/2010/03/08/is-the-increase-in-global-average-temperature-just-a-random-walk/
Hi Isaac,
Thanks for the link. I put aside my fears and read some of Bart Verheggen’s posts (the person you linked). When he says things like: “Temperatures jiggle up and down, but the overall trend is up: The globe is warming” based on running averages and, even worse, crap like this
http://ourchangingclimate.files.wordpress.com/2010/03/global_temp_yearly_p15_trendline_tavg_incl_txt_eng.png?w=675&h=441
what he’s are really saying is, “See, the chart’s going up!” Those assertions are what got me interested in this subject to begin with, to see if the data provide strong evidence for something other than “jiggling up and down.”
Not sure if you’ve heard of “technical analysis” in the financial markets. Proponents draw all kinds of trend lines over stock prices to show it’s going up or down. There’s a wonderful part in the book “A Random Walk Down Wall Street” where he shows a chart of coin flips to a technical analyst who goes nuts and says “We’ve got to buy immediately. This pattern’s a classic. There’s no question the stock will be up 15 points next week.”
Again, this isn’t to say GW2 and up are fabrications, it’s to say that we need to be cautions about our human biases, and careful in assessing the strength of our theories.
You are missing the point
http://julesandjames.blogspot.se/2012/11/polynomial-cointegration-tests-of.html
http://rabett.blogspot.jp/2010/03/idiots-delight.html
http://tamino.wordpress.com/2010/03/11/not-a-random-walk/
Now why would you try to explain away physics like this without reading up on it?
I think Mike has something here…
Get a refereed paper o this, and you will be number 25.
Good luck.
http://www.treehugger.com/climate-change/pie-chart-13950-peer-reviewed-scientific-articles-earths-climate-finds-24-rejecting-global-warming.html
I would have titled this a surprisingly weak analysis of global temperature trends.
Have a look at http://berkeleyearth.org/
Nice post. I’d like to see how well the assumption that the distribution of temperature changes is stationary holds up. Here’s one simple test: break the data into two time periods, e.g. pre-1950 and post. Then, sample only the shuffled temperature changes during the pre-1950 period and see how typical our run up was. Then repeat in the second period.
Another good thing to try would be a kernel density estimator for a piecewise linear model.
Basically, what it looks like to me is that assuming all different year to year changes were fair game to hypothetically be realized at any point back to 1881 is invalid. There will be many paths that randomly get modern-grade large YoY changes more often, artificially inflating the probability mass living above the red curve in your plots.
Your rough attempts to correct for the correlations goes a small way to studying this. But if there was some kind of feedback system making a totally different regime in the last 20 of the years, with a far different YoY distribution at that end, then just modeling first or second order correlation would not be enough to beat down that effect.
I appreciate the analogy to “technical analysis” from finance in your comment too. I agree that a lot of mainstream climate research is just marketing and professing/cheering. Don’t fall victim to any biases on this though. Read, e.g. Imbens on kernel density estimators and see if any more complex models that don’t assume so much stationarity yield good fits.
I’m a little confused here, why do we expect global climate to follow a random walk process? The strong first-order autocorrelation you’re seeing there is evidence for one of two things:
1. Last year’s climate is affecting the current year’s climate.
2. There’s a secular trend in the data!
Modelling the data as a random walk is appropriate if we believe option 1 is true. But the basics of climate science would suggest otherwise; predictable forcing (El Nino, solar cycle, GHG effect) layered on top of base geographical/biological climate patterns are the main drivers of climatic trends. While these effects are autocorrelated by nature, climate data itself is not fundamentally so.
I like your analysis (thank you for the code!), but it can’t distinguish between a real trend in stationary data and a random-walk process. If the strength of the external trend increases, the auto-correlation increase and the random-walk simulation produces more extreme results.
This is a great example how misapplication of statistical techniques can lead to nonsense and meaningless results.
Under the null-hypothesis presented here, extreme shifts in global temperature are commonplace, with 44% percent of 130 year periods under the model experiencing a temperature shift of magnitude greater than 1 degree. To put this in perspective, the 600 year shift from the “medieval warm period” to the “little ice age” was about this magnitude. There were no 130 year periods that experienced anywhere near this kind of shift.
There is little more going on here than garbage-in, garbage-out. Please refrain from posting this junk on R-bloggers.
Thanks for this. Very interesting. The big assumption you didn’t address is the arbitrary choice of start date. What if you repeated the analysis using just the last 30 or 50 years? Perhaps that’s when CO2 emmissions really accelerated.
The staring date was arbitrary, but it wasn’t my choice. 1881 is the first full year for the NASA data.
Just a quick quote from here
“Fundamentally, the argument that a time series passes various statistical tests indicating consistency with a random walk, tells us nothing about whether it actually was generated by a random process. Especially when we happen to have very good reasons to believe that it was not… “,
but that is noted, in principle, in your post.
First the math part: I have an honest question as someone who has not used Monte Carlo methods very much. Since you believe we have (negative) autocorrelation in the sequence of increments (and we better, otherwise the scaling limit is Brownian motion which has undesirable asymptotic behavior, to put it lightly), why do you still believe the empirical cdf? Without independent sampling, the ecdf might be a bad estimate of the “true distribution” of increments, and unless I’m mistaken the Monte Carlo methods you’re using all rely on treating the ecdf as an estimate of the distribution of increments.
Second, some science: briefly, you have done no science here- nothing, zip, nada. You found a (somewhat interesting) probabilistic model and concluded that this data is consistent with your model. Of course, there are many models for which the data are consistent. To apply Occam’s razor honestly you would have to posit that there exists something in nature called randomness and that thing is generating our global average temperatures, and that’s even sillier than it sounds.
This type of argument is wonderful for refuting technical analysts (especially when you set them up by showing them an actual random walk) precisely because what they do is not science either. They aren’t trying to understand anything, only predict it. Science actually tries to understand things and measures its success at doing so by its ability to predict.
Any conversation about global warming has to start with physics, not random walks. Your probabilistic model has to be constrained by known physical laws otherwise it’s not an honest model.
Third, on groupthink / peer-pressure / consensus: why do people always assume the scientific community is more likely to welcome research that confirms what it already believes? Is there any evidence for this sociological “fact”? I think scientists are actually quite excited when unexpected things happen. If someone can actually demonstrate, conclusively, that an accepted scientific theory is false, I think the community reveres that person. All great discoveries are falsifications/modifications of the previously most accepted theory. If someone conclusively refuted anthropogenic climate change they would be given a Nobel Prize, and most powerful governments and corporations in the world would be indebted to them…
Hi Matt,
As someone who is (at the moment) as agnostic as you are on this issue I appreciate a statistics-driven approach to this problem.
I was wondering if you had a chance to look at the BEST dataset (http://berkeleyearth.org/dataset/) yet, and if you’d like to comment on their analysis/conclusion?
You are confusing things which have a central limit with things which are purely a function of n(n-1) i.e. your random walk.
Over the past few days my weight has varied up and down half a pound or so in the mornings. However taking this variance – and without some drastic change in my behaviour it would be highly unlikely that my weight would go on a random walk up or down a stone or two.
There is a homeostatic mechanism that tends to keep my weight steady though varying around a level- it’s not just an iteration of the day before. Indeed if I suddenly started to lose pounds of weight without any change in exercise/diet I would worry about this surprising trend and go to see a doctor to examine potential underlying causes.
I’m sure with a moments thought you understand that global temperature is more like a homeostatic or centrally limited phenomena than that which you describe here?
Just want to chime in/pile on here. This is a very nice writeup of a completely inappropriate statistical model. The _last_ thing you’d expect surface temperature to look like is a random walk. Given the extremely consistent nature of the energy input over the millenia, you’d actually expect the data to look like a fixed (NON-drifting) value plus some sort of probably-normal noise. There’s a little bit more correlation than that because of things like volcanoes and oceanic cycles, and on multi-thousand year scales due to both solar and orbit changes, but that’s it. Any sort of multi-decadal trend in the data, such as what’s been observed over the last 50 years, is evidence that the dynamics of the system are changing. The well-documented change in CO2 in the atmosphere over that same time period, with a well understood mechanism for driving temperature, is by far the likeliest explanation at this point.
This is a nice post.
Have you looked at previous work on this?
There is a paper by A. H. Gordon,
“Global Warming as a Manifestation of a Random Walk”
published back in 1991, which was discussed by statistician Matt Briggs.
There is also this more recent paper on random walks in climate data.
Some bloggers have also run random walk simulations, see for example this one and links therein.
You are, of course, not the first statistician to look into global warming and find that the case is weak.
Matt Briggs has been saying this for years on his blog.
A significant recent paper is
“A statistical analysis of multiple temperature proxies: Are reconstructions of surface temperatures over the last 1000 years reliable?” by McShane and Wyner, 2011. The answer is no – eg they say ‘We find that the proxies do not predict temperature significantly better than random series generated independently of temperature.‘
This paper addresses a GW claim which you do not have in your list:
0. The current level of global temperature and the rate of change of temperature are unusual in historical terms.
(Links omitted to avoid going into moderation purgatory like previous comment).
You’ve done something wrong, but I’m not sure what.
If you take temps from 1980 to present, and temps from 1880 – 1980, you’ll find the average of the two periods is different. If you then shuffle all the temps and take the average of the first 40 (1980 – present) and compare that to the average of the rest (1880 – 1980), you’ll find that its very rare to get as big a difference as we get in reality. Which shows things are getting warmer, and doing so in a very non random way.
That your method does not reach the same conclusion suggests it is faulty. Though you may have accidentally shown something else interesting 🙂
Oh my, can not believe that ppl are taking this serious ad some math and ppl go crazy. Just look at the possible temperature changes doing this… and what would they be running through the whole lifetime of the earth. Physics beet nonsense all the time…
Matt,
Congratulations, this is an excellent post for illustrating why statisticians should not analyze data they don’t understand. All you have shown is that the noise in the data from year to year is larger than the trend from year to year. Your own analysis shows that the data are not homoscedastic, and yet you plod on–oblivious of the differences between different periods in your dataset. And then, despite not understanding the science or the dataset and despite your analysis not supporting your model, you state a strong conclusion contradicting that of the experts. Bravo. Might I interest you in looking into the research of the good Doctors Dunning and Kruger.
Yes we should leave the predictions to the climatologists since they are “scientists” their predictions are so good, right?
http://anthonyvioli.wordpress.com/2012/10/22/quick-post-about-failed-global-warming-predictions/
Maybe their predictions would be better if they understand the “science” of math instead.
This is an excellent blog post. It’s nice to see someone enquire into something in such an open way. I am sure that there are other people doing the same research in far more sophisticated ways – however I’ve never seen someone do so with the same transparency and at a level I can hope to understand.
On a negative point, it’s sad to see people knock your work because the conclusion disagrees with their beliefs. It disagrees with mine too, but I will seek to work out whether there is a flaw in your argument, or I am wrong.
Well done. I will be back here again 🙂
People are knocking it because his assumptions violate physics, not because his conclusions disagree with theirs.
Namely: the statistical model assumes that the earths temperature could be determined by a random walk process – it could not.
Hi Andrew, this is an argument against the very first section of the posting, which he then rejects. In the second section he looks at autocorrelations. Could the earth’s temperature not be determined by an autocorrelated process? Is the ornstein-uhlenbeck process not an example of an autocorrelated process which is mean reverting?
Matt,
One way to see that your analysis is incorrect is that it would consider all but the deepest excursions in Glacial/Interglacial periods as not significant at the 90% CL. You can draw whatever conclusions you wish from this, but I’d start to question my model.
You show that it is hard to reject your random walk null hypothesis using one particular test. Perhaps that means that the statistical test is a poor tool. Have you tested if the statistical tool works on the simulated data from a virtual world where we know that there is a strong forced signal?
It is reasonably easy to download such simulated global temperature data from the knmi climate explorer.
What a lovely post! Statistics mixed with philosophy, well set out and delightfully well written.
It reminded me of the rather infamously long VS/Bart thread – link below – which is too long to read but the statistician VS comments are worth a look http://ourchangingclimate.wordpress.com/2010/03/01/global-average-temperature-increase-giss-hadcru-and-ncdc-compared/
– J. Li is correct, variance has declined over the past couple decades.
– Of course GW won’t be an unbounded random walk, but this doesn’t establish a priori that short term changes, or even changes over the course of hundreds of years, couldn’t be viewed this way.
– The advantage of my ignorance of the science is that I can offer an independent analysis of the data. I thought this would be clear, but apparently not. If you are working off the same models and assumptions everyone else is using, it’s hard to come to a different conclusion.
– Alfredo (a commenter) posted a chart which shows that out of 13,950 peer-reviewed articles on climate since 1991, only 24 challenged the orthodox view. I thought at first this was a clever way to show the stifling prevalence of groupthink, but apparently this is being presented to prove that skeptics (of GW2? GW3? of any GW claim?) are “climate deniers” who should be dismissed outright. A question for you, the readers: do you believe the GW claims (from 2 on up) are 99.8% certain to be true? If so, which ones?
– A few of the comments and emails use an argument of the form: “We caused it, therefore it’s a trend.” This uses an assertion about causality to prove that an effect exists. Not good.
– I appreciate all of the comments, even the critical ones (the point about bounds to temperature moves is especially well taken, and I should have addressed this directly in the piece). However, no one seems willing to address the problems of falsifiability or the implied weakness of theories which are compatible with such a wide range of temperature outcomes.
Your problem here is that you’re not doing science, you’re just looking at a time series. Science includes theory and domain expertise, which you’ve chosen to ignore. Relatively simple physics says that the proper null hypothesis for the simplest possible model is a fixed temperature over time (plus noise), not a random walk. A random walk makes a specific mechanistic assumption about how the data was generated, and you’re not proposing any such thing, so don’t use it as a null hypothesis.
I’d advise you to delete this post. This is the sort of naive use of statistics that future employers may see and think poorly of.
Matt, as you are in Toronto I expect you are aware of Steve McIntyre and his blog, which often discusses statistical aspects of climate science. He wrote a post back in 2005 on random walks, with negative autocorrelation, and autoregression to deal with the boundedness question, complete with R code.
What you show here is that IF we assume that annual mean global temperature follows a random-walk, then it’s not that improbable that such a walk would produce the trend found in the temperature record since 1881. However, that just doesn’t show that your random walk hypothesis is a serious alternative to GW2. There’s some physics involved here, including the fact that a warmer earth, other things equal, emits more energy to space. But the random walk model assumes that there is no increase in the probability of a decline in global temperature when the prior year’s temperature was higher (and, on the other hand, no increase in the probability of a temperature increase when the prior year’s temperature was lower). I, for one, am glad that’s not how our planet’s climate actually works!
My, my. An “independent analysis”? You’re messing with physics here, chum. While the micro world is Heisenberg, the macro world is not. Effects have deterministic causes. That quants could crash the global economy at their whim is further proof. Finding the causes is not a statistical exercise, but a physical one. It’s just not always easy to ferret out the causes. In the case of global warming there are two facts (not theories) which matter:
– CO2 is a greenhouse gas, and larger amounts in the atmosphere raise the globe’s temperature
– humans have been loading up the atmosphere with CO2 **in addition** to any other natural sources
That there have been fluctuations, of duration longer than a few human generations, in earth’s temperature over the last 5 billion years doesn’t mean that **only** these previous causes are the **sole causes**. That’s just sophistry. The physics wins.
Further testing of assumptions is needed. In particular, a straight-forward ADF test with trend suggests that temperature changes are:
1) increasing over time;
2) negatively correlated to temperature levels (!);
3) uncorrelated to lagged temperature changes (once the effect of (2) is accounted for)
Only (3) should happen if indeed the temperature series is a random walk. If you ran your simulation analysis allowing for changes’ correlation with levels as well, your p-values would be much smaller.
I thought this was a great read, especially the in-depth discussion of your assumptions and methods. As a scientist myself, I often feel the need for more discussion of our own potential shortfalls than is usually presented in the academic journal format. I really appreciate this post.
[Disclaimer: I personally don’t come down on either side of the global warming debate.]
Regarding your methods:
I do agree with some of the commenters that a random walk is probably not the best approach when we’re talking a system so complex as surface temperature. However, just using averages over two spaces of time is not so strong, either. Neither approach allows for the complex interactions of weather patterns, solar effects, and the giant unpredictable heat sink that is our oceans. When the ozone was found to be eroding, two scientists predicted opposite results: one predicted warming where part of Earth’s heat would be reflected inward instead of escaping, and the other predicted cooling where part of the sun’s heat would be reflected away from the Earth. When a nominal increase in Earth’s average measurable surface temperature was discovered, the first theory was assumed to be completely correct. However, it is possible that both theories are correct to different degrees, and unfortunately, we currently have no way of checking.
Regarding your comment about the inverse relationship between years:
From a climate science view, this may not really make sense, but from a purely thermodynamics view, this is expected if our planet has a partial feedback loop. Due to the crazy heat capacity of water, the oceans in our planet can absorb an enormous amount of heat without us being able to detect the change. If the temperature rises, it would be expected for some heat to be absorbed by the oceans, which over time would decrease the ambient temperature. As the temperature decreases, the oceans would release some/all of the captured heat. In a closed loop, this would eventually reach steady state, but with the Earth being exposed to changing influences like the sun, moon, and rotation, the pendulum would continue to swing back and forth indefinitely. As I stated, though, this only makes sense from a purely thermodynamics perspective.
I disagree with your analysis on statistical grounds. Your methods will find no trend in even the strongest cases. see: http://blog.fellstat.com/?p=304
Ian, here is a simple example of applying the same method to data with noise and a trend. It yields a p-value of 0:
# Create random data with a clear trend plus noise
for(i in 2:1000) {
temps[i] = temps[(i-1)] + 1 + rnorm(1)
}
# What is the final amount it climbed?
observedClimb = temps[1000]
rawChanges = diff(temps)
changes = rawChanges – mean(rawChanges)
plot.ts(cumsum(rawChanges), col=”red”, ylim=c(-1100,1100), lwd=3)
trials = 1000
finalResults = rep(0,trials)
for(i in 1:trials) {
# Sample from the centered changes
jumps = sample(changes, 1000, replace=T)
# Add lines to plot for this
lines(cumsum(jumps), col=rgb(0, 0, 1, alpha = .1))
finalResults[i] = sum(jumps)
}
length(finalResults[finalResults>observedClimb]) / trials
Now you put in a huge trend- the expected yearly increase is equal to the variance of the yearly noise. Just because you can simulate examples extreme enough that your method still rejects them does not mean that your method is correct for the original problem.
There are two or three huge problems that you still haven’t addressed. First, your null model is the wrong kind of null model- as mentioned by other commenters it should be noisy fluctuation about a mean and not a random walk.
Second, even if we accept the premise of using a time series model like AR1, there are issues with the way you are simulating the increments (stationarity is a strong assumption which others have pointed out does not seem to hold, and I mentioned that you are bootstrapping data which you admit is not independent).
Third, “The fact that I don’t know any of the science just means that my analysis is independent” is not a valid reason for making important conclusions based on models which ignore physical constraints.
Joshua I’m not sure you understand significance testing. If you want the p-value to be higher than 0, then reduce the trend relative to the variance and re-run the code. If you want a fully non-significant result, set the trend component to zero (note, even then you’ll get a p-value of below 0.05 once every 20 times – that’s how this kind of testing works). My code showed that Ian’s assertion – “Your methods will find no trend in even the strongest cases” – is flat out wrong; in the “strongest cases” my method finds the strongest possible evidence.
More broadly, all random walk simulations (which this is not – read the extensive section on accounting for non-independence, and note that this is not an AR1 simulation) are bounded, as is this simulation. In the real world everything is bounded. I’m not testing the data against a platonic ideal of a random walk; I’m doing an empirical test to see if you could get equally extreme results with no trend (but equal variance and correlation).
Beyond that, I’m not sure why people are so threatened by a pure data analysis approach to the data. If the scientific theories of CO2 convinced you of GW2 and beyond, so be it. I said as much in my post. But if you start by with a model that essentially draws trend lines over temperature movements (ie the “technical analysis” nonesense), you shouldn’t be upset when someone finds the data compatible with other explanations.
Also (not to pick on you, Joshua), I’m still waiting for people to state which of the GW claims they believe and how strongly they believe them. And, while we’re at it, how about an honest assessment of the degree of falsifiability of your theories, and how the strength of these theories is impacted by the clear non-warming periods, even well into the era of industrial CO2 emmissions?
Don’t worry about my understanding. Your example refutes Ian’s wording of “even in the strongest of cases.” That was just poorly chosen wording on his part. My point still remains- run your code with 130 time steps and an expected yearly change of 1/10th the noise level and you will lose significance. That would be a more honest comparison, and your method fails to detect the trend.
Why do you say your simulation is not a random walk? It is a random walk with non-independent increments. And the point is that a random walk is a very bad model for temperatures because of its limiting behavior. To consider how bad of a model it is, consider that the random walk has already been in operation for hundreds of millions of years without causing the extinction of all life. This is not just some platonic or purely mathematical objection. You’re cheating by choosing the wrong kind of model for the phenomenon in question.
Nobody is threatened by your ability to arrive at the wrong conclusions by applying the wrong kind of model. Climate scientists are not like day-trading “technical analysts.” They are actual scientists who study the physical world. In this analogy, YOU are the technical analyst ignoring the real world, telling people not to buy because you failed to detect a certain pattern which has nothing to do with the fundamentals. Climate scientists are like a large community of economists, business analysts, accountants, and so on, who have all arrived at the same conclusion after carefully studying mountains of evidence from countless sources.
And I’ll bite: GW1-4 are almost certainly correct. For 5 I don’t know enough to say whether or not humans are the *most* significant, but I am almost certain that they are an important cause. 6 is also worded poorly so I cannot agree with it outright- but we probably have the capacity to stop the trend if not actually reverse it. The main barriers to 7 are political and that may become the greatest and most absurd tragedy in the history of our species so far. 8 is also worded poorly- unintended consequences always occur, the question is whether they will be more damaging and the answer is no. As for 9, if there are technological fixes that are actually proven to be safe then we should probably use them too, and waiting is too risky. As for falsifiability, the theory makes many falsifiable predictions. So far many of those predictions have apparently been too conservative. And unfortunately I think we are doomed to find out about the rest of them in time.
This establishes nothing. All you have shown is that the current temperature is not extreme (in the sense of being high) IF temperature is a random walk. Which is obvious to everyone who knows what a random walk is (the variance goes to infinity with the length of the time series). A mere sensible way of asking if the data is consistent with a random is to ask how likely a random walk is to generate a temperature path similar to the data. Say all points within 0.5 or 1 degree.
I did a quick CADFtest on your data:
CADFtest(theData$mean, type=’trend’)
ADF test
data: data$mean
ADF(1) = -4.4562, p-value = 0.002576
alternative hypothesis: true delta is less than 0
sample estimates:
delta
-0.353847
It seems that the hypothesis that the time series has a unit-root is strongly rejected. I guess that’s a strong evidence that assumption of temperature behaving like random-walk is a poor one.
Thanks alefsin, I was looking for a test like this.
Sune’s suggestion (as I understand it) makes good sense: what does assuming it’s a random walk imply about what we should expect regarding global average temperatures over time? Testing this against past temperature records (instrumental or proxy) would give a direct test of this hypothesis. My prediction: it fails. A vanishingly small proportion of random walks would show the kind of long-run stability our climate displays, since random walks (as the posted graph shows) tend to wander far from the starting point over time…
Yep, Bryson Brown has nailed it. Run this type of random walk for 100,000 years, and you’ll have significant probabilities for a whole range of scenarios that will *never* happen. Therefore a random walk it isn’t.
No, a random walk it is, it just ain’t no damn model of climate. The problem with this sort of approach is, as Andy Lacis points out, that climate series are subject to all sorts of annoying limitations on excursions such as conservation of energy.
I appreciate your analysis in this area. This field is difficult and in general suffers from
1. Poor definition and justification of the concept of a global temperature (how is it valid to combine disparate non equally spaced measurements taken at different times)
2. Poor cross validation of models
3. Poor predictive power of models
4. Promotion of the model itself as the science
5. Ad hominum attacks on heretics who question the consensus (good examples above)
The science was after all settled that gastric acid causes stomach ulcers …
First: When you claim that the negative 1-year autocorrelation is NOT regression to the mean, you’re wrong. The real climate system is hugely complex, and many of its components are dynamically unstable. That means that global temperatures are constantly overshooting and undershooting the equilibrium point, which is the ultimate cause of the short term variation in global temps. Those short term fluctuations are just that: regression to the mean global temperature. The problem is, the mean itself is changing, because the energy conditions that cause the temperature are changing. And ultimately conservation of energy requires the temp to come back home to where it “belongs”. Random walks do not have that real-world constraint, which is why your “simulation” doesn’t actually simulate the real world.
Nice try, though.
SECOND: If you want to take that real-world constraint into account (and that constraint is Conservation of Energy, which is a pretty big thing to ignore), instead of making the random walk non-independent (i.e., each year starts where the previous year ends) make it independent instead (i.e., each year starts at the defined overall mean — which in this case is the mean global temp as defined by CoE).
I’m guessing that you’ll have to run a whole lot of simulations to find any year that’s 7 standard deviations above the mean. Unless, of course, you add a trend. Which very nicely proves GW2.
I don’t know if it’s been mentioned in any of the articles posted, but using land temperature readings tends to understate the magnitude of temperature shift over time. The greater concentration of additional heat in the system is in the oceans, by a pretty sizable margin. You really need to use ocean temperatures to get a proper assessment.
Thank you for this. I often stand in awe at how much time I spend learning about something actually not learning about it.
This post is absolutely ridiculous. The earth’s temperature is a physical quantity that results from a radiative energy balance with space. The idea that this could be modeled with a ‘random walk’ model is just absolutely false. Please try to model a physical system with physics – not with a random number generator. If the earth’s temperature could be approximated with a random walk then it is obvious from your above graphs that the temperature would have long ago wondered out to an extreme value incapable of supporting life.
I’m very disturbed by the number of people complimenting Matt Asher for a nice analysis that is in reality anything but, for reasons clearly and repeatedly explained by numerous commenters above.
Asher has made a fundamental error of assumption of the physics involved, and is modelling something that does not occur in this universe. It’s no different to setting a sniffer dog to catch a prisoner, and all it does is track a fox across the county. Doesn’t matter how well the dog sniffs – if it can’t follow the correct scent it’s no better than a host for fleas.
I agree with Harlan. Delete this post, or at the least have the integrity to admit that this analysis is fatally and irretrievably flawed.
The article makes reference to Pascal’s Wager. I’d like to point out environmentalists use a variation of this known as the ‘precautionary principle.’ It’s easy to spot once you understand the flawed logic. The danger of this logic is how it can be used to justify any outcome you prefer.
http://www.newworldencyclopedia.org/entry/Precautionary_principle
It’s commonly used as the reason we must do something about AGW. Once you understanding the unsound logic it’s easy to spot it in action, such as in this popular clip.
http://www.youtube.com/watch?v=zORv8wwiadQ
Also note how his decision matrix lacks probability and describes outcomes that can be just one of four extremes. It assumes we can do just the right thing and there’s no downside as a result (no blackswans). It appears to be risk management to the uninformed.
More importantly it’s anti-scientific. It shifts the burden to those who must prove a negative. The fallacy is known as the ‘argument from ignorance’ and it’s the opposite of the scientific method.
Matt,
When applying statistical tests to a physical system, the physical constraints should be taken into account.
Let me offer two analogies to which there is less ideological opposition:
– If my weight gain could be statistically described as a random walk, would that mean that whatever I eat or whatever I exercise has no relevance for my weight (since, according to the stat test, it is -or rather could be- all random)?
(see also http://ourchangingclimate.wordpress.com/2010/04/01/a-rooty-solution-to-my-weight-gain-problem/ )
– Consider a boat at sea. It has both a sail (being dependent on the wind – i.e. natural variation) and an engine (i.e. radiative forcing).
The skipper puts the engine on full blast and steers the boat from, say, Holland to England.
Would anyone wonder whether it’s just the wind that’s pushing the boat over the Canal (because its movement could be described as a random walk)?
With regards to climate, it is not all that different:
“So the process of the net incoming (downward solar energy minus the reflected) solar energy warming the system and the outgoing heat radiation from the warmer planet escaping to space goes on, until the two components of the energy are in balance. On an average sense, it is this radiation energy balance that provides a powerful constraint for the global average temperature of the planet.”
In other words, conservation of energy provides a constraint on the earth’s average temperature. A random warming trend would result in a countering radiative forcing to bring the radiation budget back in balance, unless the energy is coming from other parts of the climate system (e.g. the oceans or cryosphere), which isn’t the case since they are also warming up.
If your results go against conservation of energy, chances are that your physical interpretation is incorrect.
Quoting James Annan:(http://julesandjames.blogspot.nl/2012/11/polynomial-cointegration-tests-of.html )
“Fundamentally, the argument that a time series passes various statistical tests indicating consistency with a random walk, tells us nothing about whether it actually was generated by a random process. Especially when we happen to have very good reasons to believe that it was not… “
Hi Bart,
Is it possible that, on a small enough scale, the changes in direction of your boat are essentially random?
If you start with the assumption that someone must be steering the rudder, how far “off course” would they have to get before you reconsidered your assumption?
Might there be a problem in drawing a trend line over the boats changes in direction over the past 10 minutes and saying “see, he’s turned away from Boston and is headed to Lynn”?
I’ll admit I invited some of the criticism by using the term “random walk” term, which invites complaints that idealized random walks can wander off to infinity, and also brings with it the baggage of time series analysis. I did my best in the piece to evaluate the ways in which I wasn’t treating it as a pure random walk, but it probably would have been better to call the null hypothesis: YoY changes represent a structured random process with no trend.
As with all of my posts here (see the website motto or the manifesto page), I don’t so much model (models try to see if the data conforms to platonic distributional forms) as simulate. You are correct that my ability to simulate the data as structured, trendless movements doesn’t disprove GW2, but then, I said this in my piece. However, the analyses does show that the 131 years of data themselves provides no evidence to reject this hypothesis. All of the evidence to reject has come in the form of arguments which begin with the assumption of a guy at the rudder, then state that the data doesn’t show their is no guy there!
To be as clear as possible, many of the GW claims are highly extreme, in terms of estimated temperature changes (all of the extreme predictions made 10 years ago have failed) and how we should change our lives. Do the data provide strong enough evidence to support this?
At this point, none of the proponents of the consensus views on GW have been willing to state their degree of belief in the different GW claims.
None have pointed to an alternative data set that’s more convincing (or any other data set). None have posited an alternative method that doesn’t start with an assumption of a trend then require that it be disproved.
None of the proponents have addressed the points I raised about degrees of falsifiability, biases (including our tendency to see patterns and the anthropic principle), the problematic nature of Pascal’s Wager arguments, or the possibility that the greater change in temperature in the second half of the data is purely a result of greater variance in YoY temperature changes.
Then you had better address the issue of what forcing changed the variance (hint: this is typical of physical systems whose internal energy has increased and an increase in internal energy generally means a higher temperature in thermal systems). Waving the majic wand is not an aid to understanding.
What is happening here, BTW is that to defend your analysis you are having to add more and more caveats, a sure sign of problems with the original analysis.
1) Matt, now you are inventing new terminology. “[A] structured random process with no trend?” The term random walk is not only used in the context of independent increments. What you are simulating IS a random walk. The fact that the increments are correlated does not change its asymptotics (limsup = +infty, liminf = -infty), as you can guess from looking at your plot. And again, I am not just raising this objection because of the asymptotics- but because a random walk is the wrong kind of model to use and you are effectively cheating by using it.
*** I challenge you to explain your reasoning for choosing a random walk for your simulation, instead of something like linear regression or splines.
2) “As with all of my posts here (see the website motto or the manifesto page), I don’t so much model (models try to see if the data conforms to platonic distributional forms) as simulate. … [The] data … provides no evidence to reject this hypothesis.”
What you are simulating from is a model- a random walk model with non-independent increments sampled from an empirical cdf. Your hypothesis is that the data are well-represented by this model, and you failed to reject that hypothesis. Now, leaving aside the point above that this is the wrong kind of model and that makes it unduly difficult for the data to cause rejection of the hypothesis, as others have pointed out we could still reject this hypothesis using a different statistic. The statistic you chose was just the temperature difference at the end of 130 years. That statistic is not a sufficient statistic for this model (by far- it loses a huge amount of information).
*** I challenge you to consider some other statistics and provide p-values. For example, consider the integral of the square of the sample path, and report a p-value for the probability of observing a smaller square integral than the data.
(As an aside: I think you undervalue models. Of course they are platonic, but they serve a purpose for which we don’t yet have anything better. Language serves to represent things so that we can reason about them and communicate, but nobody would mistake a definition of a chair in a dictionary for an actual chair. Similarly, careful modeling allows us to reason about things and understand them. And understanding is vitally important, it is the difference between a scientist who actually knows stuff about the real climate and a hobbyist blindly writing code and producing graphs that have no connection whatsoever to the thing he thinks he is analyzing)
3) “At this point, none of the proponents of the consensus views on GW have been willing to state their degree of belief in the different GW claims.”
Okay, I’ll bite harder this time:
1-4 all greater than 99%. I would say 100*(1-epsilon)%, but I hesitate to be that certain about a topic I don’t know much about based solely on the expertise of others, and I guess the climate may be a sufficiently complex system so that it’s possible the experts have missed something.
The remaining claims are stated in ways where I am highly certain about some aspect of them and uncertain about another. For 5, I would say greater than 95% that humans are an important cause, and I have no clue about whether they are the MOST important cause. For 6 I would say 100% that we can (hypothetically) stop the trend and maybe 80% or so that we could hypothetically reverse it (this is an off-the-cuff guess).
For 7, I would say less than 20% if “realistic” is interpreted to mean “without drastic change from the current political system.” But this is entirely a failure of politics, not economics or science or will of the people.
For 8, I guess less than 10% for unintended negative consequences being more damaging than warming itself. And I think this guess is conservative- not a tight upper bound.
For 9, say greater than 80% (again just a ball-park).
These are all very very subjective degree of belief statements and I would probably say different numbers if I were to answer again at another time.
*** I challenge you to state your own degrees of belief in the list of GW claims or any other GW-skeptic claims that you prefer over them.
4) “None have pointed to an alternative data set that’s more convincing (or any other data set). None have posited an alternative method that doesn’t start with an assumption of a trend then require that it be disproved. … None of the proponents have addressed the points I raised about degrees of falsifiability, biases (including our tendency to see patterns and the anthropic principle)”
I guess you haven’t read all the comments or something (there are quite a few of them). Of course people have suggested other data, the berkeley link for one. And other models, like the ones I mentioned above, were also brought up before (regression). The fact that regression involves a mean function does not mean it is assuming a *nonzero* trend. The question is whether the regression function is increasing over time, and you could conceivably answer “no” if the data allows that.
I specifically mentioned falsifiability, along with other commentors above. The theory of GW makes many predictions, all of which can be falsified. Or you could try to falsify any of the many intermediary scientific results that GW rests upon, such as the laws of thermodynamics- that would call into question all the models built using those laws. I also specifically mentioned biases, asking if anyone has ever demonstrated whether or not the scientific community is more likely to accept studies which confirm its existing theories or ones which disprove or establish other theories. My hypothesis is that there might actually be a bias toward constantly changing things, even unnecessarily, because of the “publish or perish” imperative.
As I recall there was a paper by Zorita on a related topic
http://www.academia.edu/2047248/Eduardo_Zorita_Thomas_Stocker_and_Hans_von_Storch_How_unusual_is_the_recent_series_of_warm_years
Matt:
I applaud your taking a fresh look at Global Warming and going to the raw statistics. The results are of course surprising given the scientific consensus that there is evidence of global warming.
This concerned me, so I too went to the NASA data that you linked to and conducted a Bayesian moving average time series analysis. The goal was to determine the distribution in the trend rate of annual changes in temperature. I allowed for the trend rate to change over time and also allowed for the standard deviation in the trend rate to change. The model that I used is:
[Temp in year t] = [temp in year t-1] + c + b(t + (n-1)/2) + theta * (change in temperature in year t-1)
where:
c= annual trend in change in temperature (the Trend Factor)
b= annual change in Trend Factor
theta = regression to the mean factor
t=1,…, 131
I also assume that the change in temperature has a standard deviation that can change over time (parameter d).
Based on my analysis, the value, c, the Trend Factor, has a 97% chance of being greater than zero. This suggests that the NASA data is strongly supportive of Global Warming.
The full results of the analysis and the code that I used can be found here:
In summary, using the same data that you used, but adopting a Bayesian approach, I get to very different results. Perhaps this is due to the way you model correlations, where the correlation between years gets “broken” after two or three years.
… here is the link to my code and full analysis results:
Code and Analysis
One correction: The model that I used is:
[Temp in year t] = [temp in year t-1] + c + b(t – (n+1)/2) + theta * (change in temperature in year t-1)
My original comment had a typo. The 97% result remains unchanged.
“To be as clear as possible, many of the GW claims are highly extreme, in terms of estimated temperature changes (all of the extreme predictions made 10 years ago have failed) and how we should change our lives. Do the data provide strong enough evidence to support this?”
Well, extreme predictions usually fail. But maybe you’d like to indicate which extreme predictions you are talking about? Is it the IPCC on atmospheric temperatures? Or sea level rise? And by saying “in the last 10 years”, aren’t you falling into the usual trap of drawing conclusions from not enough data?
“At this point, none of the proponents of the consensus views on GW have been willing to state their degree of belief in the different GW claims.”
Quite a few scientists have given likely bounds on climate sensitivity, and this is the key claim in AGW. The “skeptics” like to pretend it is 0.7C (or even 0C) for a doubling of CO2. The scientists generally go for around 2 – 3C for a doubling of CO2. There’s also some distinction between the transient response (which only includes “quick” feedbacks like humidity) and the equilibrium response that includes the long term feedbacks like changing albedo with loss of ice.
“None have pointed to an alternative data set that’s more convincing (or any other data set). None have posited an alternative method that doesn’t start with an assumption of a trend then require that it be disproved.”
But it is an almost trivial exercise to show that the assumption of no trend in the temperature data is wrong. However, if you were give the data in isolation, you would only conclude that it had increased – you would have no idea about its future behaviour. But the data is not in isolation, it is accompanied by a convincing physical rationale for a rising temperature. Put the two together, and its very hard to see anything other than a continued increase in temperatures.
Of course you should feel free to look for other explanations, but “skeptics” have been doing that for quite a few years now, and they have yet to come up with anything even remotely as convincing as AGW. What is worse, many of their attempts contradict each other, and seem mainly to exist to mislead people, rather than having any substance to them. Its almost as though the “skeptics” know that they are wrong, but are trying to convince the general public that they aren’t.
Why do you hate “skeptics”? The failure is climatologists not “skeptics”:
http://anthonyvioli.wordpress.com/2012/10/22/quick-post-about-failed-global-warming-predictions/
Now this is just getting silly. A ridiculous model, whose implications about long-term climate stability are utterly disastrous, ‘can’t be ruled out’ as a competitor with GW2 because it allows large departures from initial ‘temperatures’ without any basis in physics, and this is insisted on as a serious objection, despite the fundamental untenability of this model being pointed out in multiple comments?
Then, to pile Pelion on Ossa, the author complains that there are deep problems of falsifiability, ‘Pascal’s wager arguments’ and the new suggestion that greater year to year variance could explain the strong trend in global temperatures over the second half of the 1881 to present record.
Falsifiability is not a problem here: show that CO2 isn’t a greenhouse gas, or that the evidence for rapidly climbing CO2 levels is somehow misleading, or that the basic radiative physics is wrong, or that measures of change in outgoing LW radiation are wrong, or that … the list is nearly endless but I don’t see any chance of the challenge being taken up seriously here, where predictive models are dismissed as unsupported because non-physical tinker-toy models are “alternatives” we should consider.
Pascal’s wager starts out from the assumption that we have no evidence at all for Xianity, and argues we should believe it anyway. No one is using that kind of argument to support taking action to reduce GHG emissions. Instead, real evidence, from the basic physics to measurements confirming the impact of GHGs on downwelling LW radiation to the agreement of serious physical models that substantial warming is a very real risk, is what motivates acting now to avoid the worst-case outcomes of continued, unrestrained emissions.
Finally, if you have a credible model instead of a statistical tinker toy that gives a substantial probability to the observed trend given only increased variance, let’s see it.
Matt Asher: “The advantage of my ignorance of the science is that I can offer an independent analysis of the data. ”
OK, Matt, read that. Now, read that again. If you do not understand the context of the data–and that includes the physical system that produced it–you cannot hope to develop a meaningful analysis.
You also misunderstand the point of the graphic supplied by Alfonso. It is that even with the stakes as high as they are, that only 0.17% of articles in climate change question anthropogenic causation of the current warming epoch. If there were any controversy over the role of CO2 in climate, you would expect that to be far higher.
As to falsifiability, climate models have a very good record of successful prediction. See, for example:
http://bartonpaullevenson.com/ModelsReliable.html
Finally, as a Toronto graduate, might I commend to you the work by Jim Prall:
http://www.eecg.utoronto.ca/~prall/climate/
That would be a great response iff (if and only if) climatologists’ predictions turn out to be true.
The easiest predictions to test against reality are those made at IPCC’s first assessment report (FAR), the report that got the ball rolling. Let’s take the predictions from the FAR and compare to the data.
It can be found here :http://www.ipcc.ch/ipccreports/1992%20IPCC%20Supplement/IPCC_1990_and_1992_Assessments/English/ipcc_90_92_assessments_far_overview.pdf (this is the document that the IPCC saw fit to present to “policymakers” and clearly intends as a guide to any decisions)
The claims made here now have accrued ~ 22 years of data (and given they’re 100 years-out predictions, even 22 years seems far too little data).
Predictions:
“A n average rate o f increase o f globa l mean
temperature during the next century of about 0.3°C per
decade (with an uncertainty range of 0.2—0.5°C per
decade)” (uncertainty range is generally meant to mean 95%)
Second prediction – not applicable since action was not taken, CO2 usage has grown as assumed for “Business as usual scenario”
“an average rate of global mean sea-level
rise of about 6 cm per decade over the next century
(with an uncertainty range of 3—10 cm per decade)”
Ok now let’s connect the actual data.
A) temperature change:
Temperature rise per decade for 1990-2012 interval:
(data from http://www.wolframalpha.com/input/?i=global+climate+studies+from+1990+to+2012 )
14.2 to 14.25 or 0.05 degrees. Split over the decades we get 0.1 and -0.05 degrees.
ALL these values fall outside of the 95% certainty interval that is presented as the scientific consensus.
Now I have had this course “philosophy of science” that I distinctly recall teaching me that if predictions don’t pan out, the theory they’re based on is flawed. Granted I hated the course, but still.
B) sea level rise
data from http://en.wikipedia.org/wiki/File:Trends_in_global_average_absolute_sea_level,_1870-2008_(US_EPA).png
I read this graph as slightly under 1 inch per decade, or ~2.5 cm per decade.
Again this value is outside of the 95% interval that the IPCC’s scientific consensus gave.
So, frankly, the way I see your comment is “people who live in glass houses shouldn’t throw stones”. Maybe the statistics are wrong. But the scientific consensus is wrong, by scientific rules (wrong prediction made -> your theory is wrong).
“Is it possible that, on a small enough scale, the changes in direction of your boat are essentially random?”
And, if true, you’d then conclude that it’s possible that the engine, right there in front of your eyes, doesn’t exist, and that the boat quite likely will never cross the atlantic?
CO2 forcing is real. If you think you can disprove this basic physical fact with statistical analysis, I invite you to stare into the business end of a CO2 laser, hit the “on” switch, and report back afterwards …
Meanwhile, I have a perpetual motion machine for sale. Make me an offer …
The statistical claims of certainty about CO2 levels causing the temperature rises claimed are dependent on CO2 being the only alternative for temperatures rising.
The IPCC and AGW scientists state this by claiming all the other possible things that affect temperature cancel each other out.
Even then they admit doubling CO2 alone cannot increase temperature by 2C but will achieve this by affecting changes in water vapour, cloud and other creation of “hot spot” mumbo jumbo.
Fail.
This post wasn’t even making that strong of a statement, just saying that a random walk can’t be ruled out-
has ignited the true believers.
Apparently, infidels (like Mr. Asher) must be purged if they do not accept chapter and verse-
well done.
Scharfy, a random walk can certainly be ruled out on physical grounds unless you want to throw out conservation of energy. Several other posters have also pointed out a variety of other problems with the analysis–including that violates its own assumptions. Are the concepts of coservation of energy and self-consistency too advanced for you?
Interesting exercise and all, but the problem is that the data you’re looking at are a summary statistic of a huge physical system that follows physical laws like any other. This isn’t some particle bouncing around in a dish where we’re trying to figure out if it’s moving randomly or has a center point it’s attracted to. We KNOW there are physical laws that create a baseline expected temperature, and that if all the inputs that affect temperature don’t change, we CAN’T be observing a random walk with paths leading to wide dispersion from the expected mean equally likely as other paths that don’t deviate from the expected as much.
Think statistical mechanics. States that lead to temperatures far from the expected mean have a high free energy and are unstable and unlikely. Just taking the auto-correlation into account is a weak model for this fact.
Matt, I’m very much afraid the negative auto correlations don’t tell you very much. I did the calculation based on the data I get a value of -0.30. If you had nothing but random normal deviates to start with you would expect a value of -0.50 for the corelation. Do the math. It is the correlation between x1-x2 and x2-x3.
Hi Larry,
Yes the correlation is -0.30 or -0.32 depending on whether you compare the vector of data to itself offset by one:
cor(changes[1:129],changes[2:130])
or compare the odd and even entries of x.
I’m not sure how you got such a high amount for the expected correlation. Random noise tends to give a much lower number, try running this a few times:
x = rnorm(130)
cor(x[1:129],x[2:130])
Also, I saw the post on your blog, please note that I never claimed this method could be extended to an indefinite number of years. In general, models (or simulations) that are good over specific ranges are the norm for what we do, not the exception, no?
If you did a study of some students and found that the scores they got on their test could be modeled well with a straight regression line, should you reject that model because extending it to a student who studies 50 hours would predict the nonsensical result of 120% on their test?
Hmm, you ran your random walk model for 130 years… We have temperature data sets going back for millenia, or longer depending on what proxies you use.
What would your random walk model show for the temperature evolution of the earth over 2000 years? 200K years? 2 B years?
According to your simple statistics, shouldn’t the temperature have “walked off” one way or another by a pretty large amount by now?
I think you have shown that no one expects the earth’s temperature to follow a random walk. Good job. Now go learn some of the science and try again.
See http://www.statisticsblog.com/2012/12/the-surprisingly-weak-case-for-global-warming/comment-page-2/#comment-16453
Hi Matt
I have a few comments to your code.
Why don’t you just use column 15 in the datafile you link to? That is the annual average from December to November, and it is easy to see that it is equal to the average of the seasonal numbers you use.
But I would actually recommend you to use the Januar to December average from column 14, since then will have data for1880 also.
To get reproducible results of simulation it is a good idea to set the seed of your random number generator. I added this line before the first simulation:
set.seed(123)
I then get the fraction of trials that were more extreme than the original data to 53.7%. You should be able to reproduce that value if you set the same seed.
Btw, a lot of your code is on the same line above, so that line is extremely long, makes it a bit confusing to rerun.
Hi SRJ,
Thanks for your recommendations about the code! I’ll try to remember to set seeds and keep my line lengths reasonable. I wish R had an easy way to do multi-line comments.
Hi Matt
Another question
In the part of the code that does the Maxent stuff, why do you use the value 74 in this line:
( length(finalResults[finalResults>74]) + length(finalResults[finalResults<(-74)]) ) / trials
Shouldn’t it be the netChange that you calculate earlier?
Sorry about that, that line was old code that hard-coded the temp change from an initial (slightly different calculation) I did. Use netChange (which is 75.75).
( length(finalResults[finalResults>netChange]) + length(finalResults[finalResults<(-netChange)]) ) / trials
ad Sharfy: We’re making the point that this little exercise in statistics is not relevant to a serious discussion of climate change. If you think it is relevant, then let’s hear why. ‘True belief’ isn’t the issue– having a serious discussion is. Are you up for that?
A couple people have argued that it’s invalid to use a model for 130 years of data if that model becomes meaningless when extended to a million years. Note that if this is your argument, than you are saying that most regression analyses are invalid because they cannot be extended much beyond the existing data while still retaining meaning.
Think for a moment, do you really believe that the same simulation must work for 130 years and a million? If so, then why do we need climate change models at all when we have perfectly good weather forecasts? Why not just extend these out for the next 10 years?
A lot of the confusion stems from the thinking that I’m trying to “model the climate.” I’m not. I’m doing a simulation based on the real data, to see how extreme the observed results are relative to the yearly changes and what might happen if this empirical data represented a distribution of possible changes. If that’s not clear, please re-read the post.
Note that I’ve asked a number of questions in the comments to try and understand where those who disagree are coming from, but I can even get basic quantitative estimates of how strongly you believe in the different GW claims (thanks to Joshua for providing a qualitative estimate). Nor has anyone given any indication that failed predictions or periods of non-warming matter (thanks to Anne R. for providing a list).
One final note, there’s an inherent tradeoff between mistaking noise for signal, and missing an existing signal. Some of the complaints about the piece take the form of “If you look at it like this you can see the signal.” I don’t doubt that true, but you may also see something where there’s nothing (or only a very small signal). See my post about testing your model with fake data.
— Note that if this is your argument, than you are saying that most regression analyses are invalid because they cannot be extended much beyond the existing data while still retaining meaning.
Every stat course I took that touched on regression also stated one of the required limitations: Thou shalt not estimate beyond the data. Worth remembering.
“…you are saying that most regression analyses are invalid because they cannot be extended much beyond the existing data while still retaining meaning.”
As Robert notes, this is indeed a standard caveat in the very first lecture in regression analysis.
Show me a person who extrapolates regression data beyond the range of the independent variable and I’ll show you someone who is misapplying statistics. Moreover, I’ll show you someone who is misapplying statistics in ignorance of the complexities of the physical world.
For those who don’t understand the point, in the world of regression “as within” an independent variable does not equal “as beyond” an independent variable. Ignore this dictum at your peril.
Irrelevant distractions here from Matt. Your exercise is pointless if the alternative view of the (recent) climate record it offers is not a real alternative. No one needs the temperature record itself to rule your random walk out– it’s ruled out physically: absent substantial changes in the energy flows involved, large excursions of temperature (secular trends like the one actually observed) are not possible. Your model ignores that constraint, so it’s not a candidate and not a serious competitor for GW2. So it doesn’t show that there’s a significant probability that the climate change we’ve observed is the product of some kind of random process and not evidence of a substantial change in the forces that drive the climate.
And we know you’re not trying to model the climate. That’s the problem: what we’re talking about is the climate!
You want a response re. your various hypotheses– there’s already a pretty good one above– but I’ll bite, too:
1: yes 2: yes 3: yes (re. my understanding ‘radical’: the rate at which we’re forcing the climate is extreme, and the consequences of a 4 degree Celsius rise would be very serious; with a bit of bad luck a mass extinction on the order of the paleocence-eocene seems possible) 4: yes 5: yes (well understood radiative physics by itself makes this likely) 6: yes 7: yes (a combination of energy efficiency and aggressive deployment of low carbon energy technologies– not as big an effort as a major war, with much better payoffs) 8: yes (most side effects are improvements on present practice: health benefits from reduced air pollution, higher population densities and less sprawl occupying good farmland, …) 9: yes (I thought, from 8, that you were worried about unintended consequences? Global engineering of the kinds proposed looks very risky to me– and requires a long term, continuing effort to sustain, so long as GHG levels remain elevated, i.e. for much longer than the median lifespan of any political order the world has ever seen).
“And we know you’re not trying to model the climate. That’s the problem: what we’re talking about is the climate!”
Wow are you a troll or just really dense? I’m only in second year (biostats) and I get it. He did a simulation of global temperature and found it was indistinguishable from a random noise!
PROTIP: “quantitative means” numerical. Since you don’t give your probability for the warming claims, you must be saying “yes” I have 100% confidence in them. That’s not how science works! You don’t even care about the data or predictions. It’s like if a drug is tested vs placebo and the statistician finds no real difference only natural variation then the company says “oh our theory says it has to work because we understand the chemistry and you don’t we know there must be an effect you need to look at the data with our theory.” They say go ahead FDA approve it. We are 100% sure it works no doubt! You don’t even consider what is significant effect size. Basic stuff!
John, I would contend you do not get it. Matt is using an unphysical model to model a physical system. It is not surprising he is getting garbage.
Lol still haven’t figured out the meaning of “quantitate” I see.
You’ve put the AGW case in point form, and I’ll say that I believe in 1 – 5, and hope that the remainder are true. But as an exercise, I’ve constructed what I believe the skeptic position to be:
1) Its not warming, and anyway, its been warmer in the past
2) If it is, its natural, or it will only be small
3) If it will be big, it will be good. Warm is better.
4) CO2 is not to blame, it is plant food.
5) CO2 levels are not going up, and they’ve been higher in the past.
6) If CO2 levels are going up, its from undersea volcanoes
7) If CO2 levels are going up, and it is our fault, there is nothing we can do about it, because civilisation would collapse if we stopped burning fossil fuel
“Think for a moment, do you really believe that the same simulation must work for 130 years and a million?”
Yes, of course. The physics haven’t changed. The major problem is getting good data on solar output at the time, etc. If major forcings can be pinned down, geographical location of the continent[s], etc, then yes, we’d expect a good simulation to work over any timeframe.
“If so, then why do we need climate change models at all when we have perfectly good weather forecasts?”
Well, weather forecasting models don’t have to deal with changing forcings due to decadal fluctuations in solar output, increased forcing due to increased GHGs, Milankovic cycles, etc. On the other hand, climate models don’t have to be as concerned with precise and fine-grained data on current conditions.
You’re not making a lot of sense. And my perpetual motion machine is still for sale.
““Think for a moment, do you really believe that the same simulation must work for 130 years and a million?”
So your position is that paleoclimatologists who do use GCMs to model paleoclimate are on a fool’s errand? Because they do, you know.
A moment in google reveals that much work along these lines is being done, just one example:
http://www.geo.arizona.edu/~rees/data-models.html
Perhaps you’d like to suggest they model climate as a random walk instead?
Take a good look at the plot and play with Matt’s code and it is clear that the random walk model does not do a good job of reflecting reality.
Yes some of us have looked at it over a million year time period. Clearly it fails there. But the type of changes implied by the typical simulation over the 131 year time span imply much large temperature variations than have been seen over that time span at least since the end of the last ice age.
In addition the individual simulations imply a much greater variability even within the 131 year plots. Change he variable trial to something like 10 and change the code in the line command to something like
col=rgb(0, 0, 1, alpha = .9) so that the individual simulations show up much better. It then becomes readily apparent that every single simulation shows a much greater variability than does the red temperature line. This is clear indication that the model does not reflect what is happening in the real world.
Change trials to 1 and you can see the individual simulations. Run the code a hundred times if you want. When none of those simulations, which claim to represent what was going on with the real data, show stability in the temperatures equal to or better than the actual temperature record that is clear evidence for the failure of the model.
With the failure of the model the claims about the weak evidence for global warming cannot be substantiated.
The problem Matt has is that he has proposed a model but has failed to justify why it is a good model. He has made no attempt to validate that the model reflects the real world. And then goes on to make claims about what the failed model says about global warming.
Larry, I found your comment to be the most disappointing:
“The problem Matt has is that he has proposed a model but has failed to justify why it is a good model. He has made no attempt to validate that the model reflects the real world. And then goes on to make claims about what the failed model says about global warming.”
Matt has proposed that the current trend in global temperature can be explained by random chance. Using this model would almost never predict the actual outcome because it is nearly impossible to predict chance. We cannot model the outcome of 100 coin flips, no matter how well we understand the coin or the mechanics of flipping it. But we can calculate that 51 heads and 49 tails does not a biased coin make.
Matt – I actually think it is an interesting academic exercise to see if you can tell if that data was randomly generated (without any understanding of the physics) – there was a few arguments that I thought were interesting that I don’t think you have addressed
1) the ADF test that alfesin mentioned
2) the Bayesian moving average time series analysis that Howard mentioned
3) the Eduardo Zorita paper that I mentioned
“It considers the likelihood that the observed recent clustering of warm record-breaking mean temperatures at global, regional and local scales may occur by chance in a stationary climate. Under two statistical null-hypotheses, autoregressive and long-memory , this probability turns to be very low: for the global records lower than p= 0001, and even lower for some regional records. The picture for the individual long station records is not as clear, as the number of recent record years is not as large as for the spatially averaged temperatures.”
(I didn’t mean to post this as a reply to an earlier comment, but as a new comment. Sorry for the double post)
1) Matt, now you are inventing new terminology. “[A] structured random process with no trend?” The term random walk is not only used in the context of independent increments. What you are simulating IS a random walk. The fact that the increments are correlated does not change its asymptotics (limsup = +infty, liminf = -infty), as you can guess from looking at your plot. And again, I am not just raising this objection because of the asymptotics- but because a random walk is the wrong kind of model to use and you are effectively cheating by using it.
*** I challenge you to explain your reasoning for choosing a random walk for your simulation, instead of something like linear regression or splines.
2) “As with all of my posts here (see the website motto or the manifesto page), I don’t so much model (models try to see if the data conforms to platonic distributional forms) as simulate. … [The] data … provides no evidence to reject this hypothesis.”
What you are simulating from is a model- a random walk model with non-independent increments sampled from an empirical cdf. Your hypothesis is that the data are well-represented by this model, and you failed to reject that hypothesis. Now, leaving aside the point above that this is the wrong kind of model and that makes it unduly difficult for the data to cause rejection of the hypothesis, as others have pointed out we could still reject this hypothesis using a different statistic. The statistic you chose was just the temperature difference at the end of 130 years. That statistic is not a sufficient statistic for this model (by far- it loses a huge amount of information).
*** I challenge you to consider some other statistics and provide p-values. For example, consider the integral of the square of the sample path, and report a p-value for the probability of observing a smaller square integral than the data.
(As an aside: I think you undervalue models. Of course they are platonic, but they serve a purpose for which we don’t yet have anything better. Language serves to represent things so that we can reason about them and communicate, but nobody would mistake a definition of a chair in a dictionary for an actual chair. Similarly, careful modeling allows us to reason about things and understand them. And understanding is vitally important, it is the difference between a scientist who actually knows stuff about the real climate and a hobbyist blindly writing code and producing graphs that have no connection whatsoever to the thing he thinks he is analyzing)
3) “At this point, none of the proponents of the consensus views on GW have been willing to state their degree of belief in the different GW claims.”
Okay, I’ll bite harder this time:
1-4 all greater than 99%. I would say 100*(1-epsilon)%, but I hesitate to be that certain about a topic I don’t know much about based solely on the expertise of others, and I guess the climate may be a sufficiently complex system so that it’s possible the experts have missed something.
The remaining claims are stated in ways where I am highly certain about some aspect of them and uncertain about another. For 5, I would say greater than 95% that humans are an important cause, and I have no clue about whether they are the MOST important cause. For 6 I would say 100% that we can (hypothetically) stop the trend and maybe 80% or so that we could hypothetically reverse it (this is an off-the-cuff guess).
For 7, I would say less than 20% if “realistic” is interpreted to mean “without drastic change from the current political system.” But this is entirely a failure of politics, not economics or science or will of the people.
For 8, I guess less than 10% for unintended negative consequences being more damaging than warming itself. And I think this guess is conservative- not a tight upper bound.
For 9, say greater than 80% (again just a ball-park).
These are all very very subjective degree of belief statements and I would probably say different numbers if I were to answer again at another time.
*** I challenge you to state your own degrees of belief in the list of GW claims or any other GW-skeptic claims that you prefer over them.
4) “None have pointed to an alternative data set that’s more convincing (or any other data set). None have posited an alternative method that doesn’t start with an assumption of a trend then require that it be disproved. … None of the proponents have addressed the points I raised about degrees of falsifiability, biases (including our tendency to see patterns and the anthropic principle)”
I guess you haven’t read all the comments or something (there are quite a few of them). Of course people have suggested other data, the berkeley link for one. And other models, like the ones I mentioned above, were also brought up before (regression). The fact that regression involves a mean function does not mean it is assuming a *nonzero* trend. The question is whether the regression function is increasing over time, and you could conceivably answer “no” if the data allows that.
I specifically mentioned falsifiability, along with other commentors above. The theory of GW makes many predictions, all of which can be falsified. Or you could try to falsify any of the many intermediary scientific results that GW rests upon, such as the laws of thermodynamics- that would call into question all the models built using those laws. I also specifically mentioned biases, asking if anyone has ever demonstrated whether or not the scientific community is more likely to accept studies which confirm its existing theories or ones which disprove or establish other theories. My hypothesis is that there might actually be a bias toward constantly changing things, even unnecessarily, because of the “publish or perish” imperative.
— My hypothesis is that there might actually be a bias toward constantly changing things, even unnecessarily, because of the “publish or perish” imperative.
Historically, more the other way. Three points.
1) Einstein’s theories were not rapidly accepted, since they conflicted with Newton, and everyone else.
2) Einstein resisted quantum mechanics, because he didn’t believe in the premise (God playing at dice, and all).
3) Standard dictum: data doesn’t invalidate a theory, but another theory does.
3) may sound odd to the youngsters, but it’s been an article of faith for hundreds of years. Science doesn’t toss a theory based on some contradictory data. A theory gets tossed when a proposed theory explains both the data explained by previous theory as well as data only explained by the proposed theory. This is why it’s the “theory” of evolution. Saying “God did it” for either evolution or climate change doesn’t cut it.
Publish or perish has led, given the explosion in population which includes Ph.Ds, to a lot of dancing on pinheads. Fundamental theory disputes largely ignore all of that.
Your first point is not correct.
According to Wikipedia. special relativity was widely accepted within 6 years of publication:
Eventually, around 1911 most mathematicians and theoretical physicists accepted the results of special relativity. …
And experimental confirmation of general relativity was coming in as early as 1919, only four years after Einstein’s final version in 1915.
Your second point is irrelevant, a physicist is not physics, and so what if Einstein wouldn’t accept QM?
“1) Einstein’s theories were not rapidly accepted, since they conflicted with Newton, and everyone else.”
On the contrary, within five years of publishing his paper on special relativity, “most mathematicians and theoretical physicists accepted the results of special relativity”. (http://en.wikipedia.org/wiki/History_of_special_relativity#Early_reception)
Physicists knew Newton’s theories were wrong long before then due to experimental evidence and Einstein’s work was the culmination of much effort to resolve that problem.
“2) Einstein resisted quantum mechanics, because he didn’t believe in the premise (God playing at dice, and all).”
He did, however, receive the Nobel Prize for his 1905 paper on the photoelectric effect, which effectively *established* quantum theory. What he *resisted* was the premise that quantum theory is complete and that there are no local hidden variables that, if known, would explain away the apparent randomness. It wasn’t until 1981 that experiments convincingly proved John Bell’s 1964 theory that there are no (local) hidden variables, both well after Einstein’s death. His “resistance” is therefore a lot more subtle than you suggest.
“3) Standard dictum: data doesn’t invalidate a theory, but another theory does.”
That depends on both the data and the theory in question. A well-established theory that has stood the test of time and made countless correct predictions isn’t going to be tossed overnight because of one experiment that contradicts it. Remember “cold fusion”, an experimental result that seemingly overturned known physics?
Furthermore, even though a theory is known to be wrong — as both the Standard Model and Relativity are known to be — doesn’t mean the theory isn’t *useful*. We just have to know under what circumstances each is valid, and tread very carefully when dealing with situations where both apply (e.g. singularities).
Conclusion that statistical analysis with random walk fails to find evidence of global warming is correct but seems incomplete. How strong is this conclusion?
What is missing is an experiment that applies the same method on data with known trend and same variance.
For instance, if we measure the temperature in a thermostat that keeps it between T1 and T2, the temperatures will go up and down over time. Random walk permutations will go far beyond T1 and T2. If T1 and T2 are changing over time how extreme the trend should be for this analysis to detect it? One can use synthetic data generated in the same R program with the same variance. I am afraid that for all but a few extreme trends this analysis will come to the same conclusion – no evidence of a trend. But again – such experiment is missing.
John Rogers (December 6, 2012 at 6:26 am)
“He did a simulation of global temperature and found it was indistinguishable from a random noise!”
No he didn’t John. He made 1000 runs of a random walk model that produced a large envelope of outputs one of which (or a subgroup of which) could be selected as being coincidentally similar to the actual progression of surface temperature.
Your “PROTIP” example is not a good analogy ‘though it does perhaps have an ironic relationship to Matt’s analysis. The FDA wouldn’t approve a drug based on lack of efficacy relative to a placebo. On the other hand (and we know this happens occasionally), a drug might be approved under circumstances that the company was aware of a problem with respect to side effects, or had given the pretence of efficacy by using trials with flawed designs. The key point in assessing drug efficacy is Hard Unbiased Information.
The same applies to understanding the Earth temperature evolution. If we’re interested in attribution/causality, we obviously take into account the fact that the troposphere has warmed while the stratosphere has cooled (indicating enhanced greenhouse effect), that the surface warming is associated with the vast and progressive increase in ocean heat content (i.e. not a “random walk” at all), and all of the other physical signatures that informs our understanding.
No doubt one could also model the progression of a quantitative parameter of a person’s cancer (for example) as a “random walk” but you’d be unlikely to convince knowledgeable people that cancers are the products of the accumulation of random fluctuations of cell mass without causality.
Reminiscent of McIntyre’s and McKitrick’s attempt to vanish the hockey stick…
It seems to me that “average yearly surface temperature” is not just an abstract philosophical notion, but rather a physical property. Any physical property is dependent on other physical properties, and therefore cannot be analyzed in isolation.
How does this “random walk” model of yours account for other related properties? Energy in the system comes to mind, as energy and temperature are very closely related. If the temperature increase is just a random walk, where did the required energy come from? Was it the energy going on a random walk, which was the actual basis of the temperature change? Is it possible for energy to randomly change?
Matt,
Thanks for the comments you posted over on my blog. I responded directly to those there, and if someone is interested in that exchange I trust they can find their way of there.
But I wanted to expand on some of the what has been said and to say I think the issue of going beyond the original 131 is getting in the way of understanding the deficiencies in your model.
Others have taken the original 131 year data set and applied a CADF test and found that it rejects a claim that the series is a random walk. I would think that would also make it clear that modeling using a random walk to see if the trend is “significant” would be ruled out.
Let me take it from the other side. You have created 1000 simulations of the time series based on the random walk model. So you have a distribution of potential outcomes if in fact the random walk was a good model. So I ask the question is it reasonable to conclude that the actual time series arose from the simulated distribution.
In very simplistic terms if I assumed that a variable was from a N(0,1) distribution(your simulation) than obtained an observation x(the actual time series) can I conclude that x came from that distribution. If x=1.2 then certainly it could have come from there, but if x=1000 it is very unlikely to have come from there.
Your set of simulations provide a base distribution of outcomes. As an evaluator I want to focus on the variability of the time series. My actual measure is the difference between the maximum and the minimum temperature during the 131 year period.
For the base data this is
max(theData$means)-min(theData$means)
which yields a value of 107.
Then I calculate this same value for each of the 1000 simulations. To do this I add the following code to your program.
set.seed(123)
This way you can duplicate my numbers if you wish.
Just prior to the for loop add the two lines:
jump.max <- rep(0,trials)
jump.min <- rep(0,trials)
I use these variables to capture the spread of the temperature range for each simulation.
Inside the for loop add the lines:
running.sum <- cumsum(c(0,jumps))
jump.max[i] <- max(running.sum)
jump.min[i] max(theData$means)-min(theData$means))
This will give a count of the number of cases in the simulation where the difference between the minimum and maximum temperature is greater than 107. The range in the original data. The result I got is 963.
That is over 96% of the simulations had a greater variability than does the original time series, using this measure, is pretty conclusive to me that the original time series does not follow the distribution that results from your model.
Again I am force to reject the hypothesis that a random walk models the temperature over the last 131 years.
I see I mixed up my code a bit. Must have cut somewhere at the wrong time.
In the for loop the code is:
running.sum <- cumsum(c(0,jumps))
jump.max[i] <- max(running.sum)
jump.min[i] max(theData$means)-min(theData$means))
It is this last line that gives the value of 963.
Hi Larry,
I think the comment parser at wordpress messes up some of the code.
Did you try adding your code to the MaxEnt version, which bakes the covariance back into the data? I just did this and the number of trials which exceeded the observed range was about 80%, still perhaps uncomfortably large, but much less concerning than 96%. I used set.seed(345) and 1000 trials for this.
Your point about the range of the trials being similar to the original is interesting though and worth more consideration. Because the original data dips so little before heading up, the total range isn’t much above the final result (0.76). Thus, anytime the simulation yields a more extreme result, it’s likely to also have a larger range, no?
I must admit that the CADF details are new to me. At this point it’s clear that I shouldn’t have used the “random walk” term, since right away people start thinking AR and ARMA and Gaussian noise and all these other things and then get upset with the idea of applying this to climate, even over (relatively) short periods of time. Unfortunately, calling the method a “bootstrap of centered empirical temperature changes adjusted for observed data structures” probably wouldn’t have helped with comprehension.
Sorry should have begun by saying that I understood what you were doing with the code and implemented it. Here’s what I used:
running.sum = cumsum(c(0,jumps))
jump.range[i] = max(running.sum) – min(running.sum)
inside the loop, with:
jump.range <- rep(0,trials) outside the loop.
Matt, I did all my coding and testing on your first set of data before you played with the adjustments for the negative correlations.
I had two reasons for that. First you had said the adjustment did not make any fundamental differences in your conclusions. And second I never saw the need for doing the adjustment due in the problems I saw with the data model. I also expected a negative correlation. You are actually calculation the correlation between x(1)-x(2) and x(2)-x(3). If the observations are random then the correlation will be negative.
Yes the 80% number is not quite the concern as is the 96% figure I got. Keep in mind thought that if there is a trend in the data then the range in the actual data is going to be higher than in a stationary climate situation. The way you build your simulations there is no “real trend” except what a random walk tends to create. I view the 96% and the 80% to be biased downward due to what I see as a real trend in the actual data set.
Frustration. I know I cut and pasted right the second time. One last try. The jump.min code is the same as the jump .max code except that is used the min function
The last line of code is outside of the for loop. It subtracts jump.min from jump.max to get the range and computes the number of times that values is greater than 107.
Hope that works….
Firstly, for an R post nice code and graphs and everything.
However, for a GW post – shame on you. The title is incredibly misleading, you redeem yourself by pointing out that YoY global averages are meaningless yet everything prior to that can be used by ‘GW deniers’ (read: big oil companies, governments not wanting to spend money etc. etc.) as ‘evidence’.
You already state that you don’t have the required background to be claiming that there is only a weak basis for global warming, yet make that claim anyway – shame. How can you honestly expect to get a decent idea if what is going on using only an average temperature for the whole planet per year (“I’m only considering the yearly average temperature”), that average is almost meaningless on its own, not to mention the data from the early years is far less reliable.
GW causes among other things more extremes in temperature, eg. colder winters, warmer summers and more intense storms, these things are lost when taking an average.
The scientific evidence (that you admit to not even knowing) is overwhelming, it is not a bunch of people following the pack, that is not how science works. A real science article would reference the rising ocean levels, increasing CO2 levels and all the other evidence that shows global warming is real. Cherry picking one small peice of a very large puzzle is not real science.
In addition your mention of Pascal’s wager is not apt here, in that wager what you lose is a life time of pleasure (a pretty big deal to most people). In this argument if we act according to GW being real and man made and it turns out to either not be real or not man made then what do we actually lose? Nothing, money gets spent making the planet much greener, less cancer causing pollution etc. To claim that would be a waste of time and money is incredibly short sighted, criminal almost.
— How can you honestly expect to get a decent idea if what is going on using only an average temperature for the whole planet per year (“I’m only considering the yearly average temperature”), that average is almost meaningless on its own, not to mention the data from the early years is far less reliable.
As the canard goes, “one foot in a lava stream, the other on a glacier; comfortable on average”.
The mention of Pascal’s Wager is valid, but lacks the broader context of the precautionary principle. This is the logic of the environmental movement. See my comment on this from Dec 5th.
You’re argument is flawed in that it assumes “doing something” has no costs and no risks (no black swans). You’re assuming “doing something” can only have good outcomes. You’re position is the environment trumps everything else, and use the precautionary principle to smuggle in your desire for “doing something” (whatever that may be).
So, as you see a bad collision approaching, you would refuse to step on the brakes because you couldn’t be sure that wouldn”t somehow make it worse?
We have (if you’re prepared to actually look at the evidence seriously) powerful evidence that our GHG emissions pose a terrible threat to the climate and oceans we depend on. And you think doing something about it is a bad idea because something or other just might go wrong? That’s some serious crazy in my book.
You’re assuming you know the climate as well as you know your automobile. You’re assuming you know what are the “brakes” and this will only stop or slow you down with no other effect. You’ve not even suggested what this “brake” would be. So it’s impossible to assess the risk or costs of “doing something.”
I made no such assumption– maybe you’re unfamiliar with the use of metaphor? There are plenty of obvious things to do, beginning with rapid, ongoing reductions in our use of fossil fuels. Energy efficiency (for vehicles, buildings, industry), development of non-fossil fuel based energy sources (already competitive in many applications) and quite possibly development of next-generation nuclear energy systems (thorium, for instance, is a safer fuel cycle, very difficult to divert to weapons production). All these things are well within current technology, and the easy ones are economically superior to current practice already (even ignoring the externalities associated with fossil fuels).
Instead, we continue to insist on subsidizing fossil fuel development (a mature and very profitable industry with reserves large enough to commit us to 5 or 6 degrees C of warming, perhaps as early as the end of the century. Our agricultural systems won’t survive that in anything like their current form– and acidification of the oceans threatens them as a food source too.
Impossible to assess? The only alternative to burning fossil fuels until they’re all gone is to jump down a dark well of mystery? Why not actually look at the plans and proposals out there? The ‘wedge’ strategy (combining conservation with multiple new energy sources over time); proposals to cut vehicle fuel consumption by 50% in the next 10-15 years (well within current technology); proposals for thorium fueled reactors; continued improvement in wind power systems… the notion that it’s all just unknowable is pure fear-mongering.
Once again, you did not make any mistake by calling it a random walk. IT IS A RANDOM WALK (with correlated increments). Everything that is true generally about random walks (without assuming independence of increments) is true about your model.
Also, the max-min statistic gets more information but still is not even close to being a sufficient statistic. Try the integrated square, or integrated absolute value. Just sum(x^2)/131 where x[i] = temp at time i.
Joshua,
The sum of the squared deviations looks to me to be a better measure than the range statistic I used. It better captures what is going on for the entire time series.
As noted, this analysis is of the land and sea surface records, which have been averaged together. This is the flaw of one foot in a lava stream, the other on a glacier where on average one is comfortable. But it’s actually worse than that.
Averaging them together is like averaging the temperature of a balloon and a bowling ball. They have the same volume, but they’re not equal. The density of water is much greater than air. The temperature in my bathroom is not the average of my cold bath water and the air coming from my hair drier. Air requires much less energy to warm than water. The problem is assuming temperatures are equal measurements of energy.
I have a distrust of the land-based temperature records. First, these records are effected by land management, urban development, tall buildings, etc. Knowing the “normal” temperature from these areas is unlikely. We also have a alternative state of the art system (USCRN) unaffected by such factors and it’s shown the commonly used land based data you’ve used is significantly effected with a warming bias.
Secondly, these land based records have a history of being quietly adjusted (at least I haven’t found an explanation). These adjustments would create a warming trend even if the source were random noise. The past has been made cooler, and the more recent years have been made warmer.
Simply compare the land and the sea surface record from 1880 to the present. Presumably they should be similar. Yet you’ll find the land temperatures from 1980 have been significantly warming that over the sea. That alone causes me to question the reliability of land based temperature data.
I prefer to examine the sea surface temperatures in isolation. It’s not effected by factors that occur on land. Plus the air can more more freely, making it homogenous. It’s less prone to variability. More importantly the oceans are the planet’s main store of energy. The temperatures of the ocean waters and air are not equal, and cannot be average together. Unfortunately we don’t have long-term records of the ocean’s temperature, but we do have air temperatures at the sea’s surface (which is at least something better than our land temperature records).
I’m not a statistician and I cannot apply your code to the available data. The data is also provided in more detail. You can get monthly temperatures of the sea surface going back to 1880, and even for specific long/lat grids.
In my amateurish analysis of sea surface temperature I find a warming trend that began in 1909 rising 0.68 degrees C in 35 years. Then temps dropped dramatically, for some inexplicable reason, in just four years erasing nearly half of that warming. Presumably this was natural and not due to AGW since the level of CO2 was not yet significant.
To be generous, if we say the next warming trend begins at the coldest point in 1948 and continues to the present. There’s been less warming and over a longer period of time (50 years to climb 0.6 degrees C). In other words, the warming that began in 1909 shows a naturally occurring phenomena that exceeds what is claimed by the AGW theory. The conclusion is current warming isn’t unusual, even with the significant increase of CO2 in recent years (1/3rd has been released since 1998).
Hopefully someone with the statistical skills I lack can better analyze the data. It can be found here:
http://climexp.knmi.nl/select.cgi?id=someone@somewhere&field=hadsst2
http://www.metoffice.gov.uk/hadobs/hadisst/data/download.html
Quick question:
Since you used the observed YoY changes over the whole dataset to set your parameters, aren’t you just basically just re-creating the dataset with some stochasticity? You’re essentially saying that the observed trend is no different from a randomized version of the past 130 years.
You should probably use the first 50 years or so to set your parameters and then see if the rest of the dataset deviates from that model.
Hi Dai,
The key difference is that the data have been centered before resampling. The clearer the trend in the original data, the less likely a centered resampling will achieve equally extreme results.
Even if you’ve centered the data, your problem is still there. The mean value you are subtracting from is also part of the overall trend of increasing temperature. So you are still essentially saying that GIVEN what we have already observed, the temperature change over the past 130 years is non-random.
Hi Dai,
I don’t understand your point. Try the code I posted here:
http://www.statisticsblog.com/2012/12/the-surprisingly-weak-case-for-global-warming/comment-page-1/#comment-16404
and play around the numbers to see how with this centering method if you strengthen a trend you get a lower p-value, and vice versa.
The analyses you present would make some sort of sense for a purely observational study of an unknown phenomenon. I’m an epidemiologist and I do this sort of analysis all the time.
In my spare time I do a bit of demography, where the ‘physics’ of the system are quite well understood. People are born, they migrate, and they die. All my work on demography is based on this well understood model.
This is, I gather, how people who know the subject analyse climatology data. Please understand that you can no more analyse climate data in splendid isolation, than I can anlyse demographic data, ignoring the processes that lead to my populations.
Anthony
WHY THERE IS GLOBAL WARMING
People in the USA, are being told by the U.S. government and media that global warming is man-made. If that is true, how can the government and media explain the high temperatures the earth has experienced in past years when there were far fewer people? Let us look back in the world’s history: for example, between roughly 900AD and 1350AD the temperatures were much higher than now. And, back then there were fewer people, no cars, no electric utilities, and no factories, etc. So what caused the earth’s heat? Could it be a natural occurrence? The temperature graph at the bottom of this article shows the temperatures of the earth before Christ to 2040.
In the book THE DISCOVERERS published in February 1985 by Daniel J. Boorstin, beginning in chapter 28, it goes into detail about Eric the Red, the father of Lief Ericsson, and how he discovered an island covered in green grass.
In approximately 983AD, Eric the Red committed murder, and was banished from Iceland for three years. Eric the Red sailed 500 miles west from Iceland and discovered an island covered in GREEN grass, which he named Greenland. Greenland reminded Eric the Red of his native Norway because of the grass, game animals, and a sea full of fish. Even the air provided a harvest of birds. Eric the Red and his crew started laying out sites for farms and homesteads, as there was no sign of earlier human habitation.
When his banishment expired, Eric the Red returned to congested Iceland to gather Viking settlers. In 986, Eric the Red set sail with an emigrant fleet of twenty-five ships carrying men, women, and domestic animals. Unfortunately, only fourteen ships survived the stormy passage, which carried about four-hundred-fifty immigrants plus the farm animals. The immigrants settled on the southern-west tip and up the western coast of Greenland.
After the year 1200AD, the Earth’s and Greenland’s climate grew colder; ice started building up on the southern tip of Greenland. Before the end of 1300AD, the Viking settlements were just a memory. You can find the above by searching Google. One link is:
http://www.greenland.com/en/about-greenland/kultur-sjael/historie/vikingetiden/erik-den-roede.aspx
The following quote you can also read about why there is global warming. This is from the book EINSTEIN’S UNIVERSE, Page 63, written by Nigel Calder in 1972, and updated in 1982.
“The reckoning of planetary motions is a venerable science. Nowadays it tells us, for example, how gravity causes the ice to advance or retreat on the Earth during the ice ages. The gravity of the Moon and (to a lesser extent) of the Sun makes the Earth’s axis swivel around like a tilted spinning top. Other planets of the Solar System, especially Jupiter, Mars and Venus, influence the Earth’s tilt and the shape of its orbit, in a more-or-less cyclic fashion, with significant effects on the intensity of sunshine falling on different regions of the Earth during the various seasons. Every so often a fortunate attitude and orbit of the Earth combine to drench the ice sheets in sunshine as at the end of the most recent ice age, about ten thousand years ago. But now our relatively benign interglacial is coming to an end, as gravity continues to toy with our planet.”
The above points out that the universe is too huge and the earth is too small for the earth’s population to have any effect on the earth’s temperature. The earth’s temperature is a function of the sun’s temperature and the effects from the many massive planets in the universe, i.e., “The gravity of the Moon and (to a lesser extent) of the Sun makes the Earth’s axis swivel around like a tilted spinning top. Other planets of the Solar System, especially Jupiter, Mars and Venus, influence the Earth’s tilt and the shape of its orbit, in a more-or-less cyclic fashion, with significant effects on the intensity of sunshine falling on different regions of the Earth during the various seasons.”
Read below about carbon dioxide, which we need in order to exist. You can find the article below at:
http://www.geocraft.com/WVFossils/ice_ages.html.
FUN FACTS about CARBON DIOXIDE.
Of the 186 billion tons of carbon from CO2 that enter earth’s atmosphere each year from all sources, only 6 billion tons are from human activity. Approximately 90 billion tons come from biologic activity in earth’s oceans and another 90 billion tons from such sources as volcanoes and decaying land plants.
At 380 parts per million CO2 is a minor constituent of earth’s atmosphere–less than 4/100ths of 1% of all gases present. Compared to former geologic times, earth’s current atmosphere is CO2- impoverished.
CO2 is odorless, colorless, and tasteless. Plants absorb CO2 and emit oxygen as a waste product. Humans and animals breathe oxygen and emit CO2 as a waste product. Carbon dioxide is a nutrient, not a pollutant, and all life– plants and animals alike– benefit from more of it. All life on earth is carbon-based and CO2 is an essential ingredient. When plant-growers want to stimulate plant growth, they introduce more carbon dioxide.
CO2 that goes into the atmosphere does not stay there, but continuously recycled by terrestrial plant life and earth’s oceans– the great retirement home for most terrestrial carbon dioxide.
If we are in a global warming crisis today, even the most aggressive and costly proposals for limiting industrial carbon dioxide emissions and all other government proposals and taxes would have a negligible effect on global climate!
The government is lying, trying to use global warming to limit, and tax its citizens through “cap and trade” and other tax schemes for the government’s benefit. We, the people cannot allow this to happen.
If the Earth’s temperature graph is not shown above, you can see this temperature graph at the link:
http://www.longrangeweather.com/global_temperatures.htm
>>>People in the USA, are being told by the U.S. government and media that global warming is man-made. If that is true, how can the government and media explain the high temperatures the earth has experienced in past years when there were far fewer people?<<>>CO2 that goes into the atmosphere does not stay there, but continuously recycled by terrestrial plant life and earth’s oceans– the great retirement home for most terrestrial carbon dioxide.<<>>If we are in a global warming crisis today, even the most aggressive and costly proposals for limiting industrial carbon dioxide emissions and all other government proposals and taxes would have a negligible effect on global climate!<<<
This smells like a PR guy being paid to post nonsense.
Does the change in temperature need to strongly support the presence of global warming for us to to be compelled to action? I do not understand why you have assumed this is a prerequisite. To me, you have applied statistical analysis properly in one sense, but have used it to draw a fallacious broader conclusion.
We can be compelled to action by weak evidence. But given weak evidence, how much action is appropriate? What kind of actions should you take? And, most importantly, how do you know that action you take (which by many estimates will cost trillions of dollars) won’t in some way make the world worse off, if in no other way than by opportunity costs?
For example, suppose that in the next hundred years there’s a one in a million chance we get hit by a humanity ending asteroid. That’s a way worse outcome than a 4 degree temperature rise. What if we uncover some other threat we believe to have a one in 900,000 chance of wiping out humanity? Should we take all our resources and devote them to that risk instead? But wait, there’s really no such thing as “our resources”, only resources owned (or controlled) by various people and entities. If the only way to get every nation to reduce CO2 emissions by half results in a heightened risk of global war (another way worse consequence than a 4 degree rise), should we go forward anyway? The unknown risks of radical change (especially change that forcibly reduces living standards by making energy much more expensive), could be much higher than the risk of man-made global warming.
I still don’t see any response from Matt to the comments pointing out the importance of physical constraints like conservation of energy here. Without a serious answer to those challenges, this purely statistical model can’t be interpreted as telling us anything at all about climate and its recent changes– it’s a purely numerical exercise, not a climate model.
It will take some study to fully understand the examination being made.
Never the less, the standard hypothesis test answers the question quite simply.
The hypothesis is, given the variance about the mean rate of change, does this mean rate of change differ from zero sufficiently to conclude that it is highly unlikely to be zero.
A linear regression is done and the p-value is calculated for the slope coefficient. This is compared to a random distribution centered about zero and the probability of getting a value as extreme is calculated. Generally, we take 95%/2 or 99%/2 as our alpha (it’s a one sided test.)
And, in fact, the slope is large enough, given the variance, that it is highly unlikely to be the result of a random distribution about zero.
The biggest hole I see in the analysis is the limited data set of surface temperature. My understanding is that much of the global warming created by elevated CO2 levels have been absorbed by the Earth’s oceans, acting like a huge global battery being charged up. Another major factor was the albedo effect of the growing smog created by particle pollutants in the atmosphere coinciding with growing CO2 levels, now being removed from the atmosphere. Since hte 1970s we’ve gone from an Earth’s average albedo of 0.39 to 0.3.
Even so, you admit “Clearly, temperatures have risen since the 1880s. Also, volatility in temperature changes has increased.” You seem to have drawn conclusions with far from complete data. Interesting exercise, but generally meaningless.
Good points about our limited data. That was one of my main frustrations doing the analysis.
The point of statistics IS to draw conclusions from incomplete data, that’s all we ever do 🙂
In this case the conclusion is: Based on available data, the case for catastrophic AGW appears much weaker than many claim. That’s not a strong claim, but it’s not a meaningless one.
One more note this post is now over 4 years old, even though that’s not a huge amount of additional data (relative to the cumulative past), it’s time to redo the analysis and include the most recent data.
There are physical constraints here that this statistical model ignores, starting with conservation of energy. Change in global temperature is not a random walk.
It’s interesting but incomplete. You used one kind of data to analyze an incredibly complex system and then claimed that we can’t show that GW 2-9 are valid claims. If you really want to draw conclusions about GW, you need to consider other sources and a more comprehensive set of data with different metrics (e.g. ocean temperatures, etc). I think this post really drives home the idea that analysis without context can be dangerous. You should make sure you understand or you are working closely with others who understand the system you are analyzing. It’s short sighted and arrogant to claim that your one-dimensional analysis disproves the conclusions of climate science. And no one wants climate change to happen. But something is happening, ice is melting, water is rising, weather is changing, disasters are more frequent, insects and animals are dying. There are surely many many causes, these are wicked problems, but changing temperatures is one realistic idea that has been supported by other more comprehensive analyses and modeling, that is supported by physics, dynamics, etc.
You need to understand the system your are looking at and the different metrics for measuring it. Science matters too.