Probability and statistics blog

Uncategorized — Comments Off
28
Apr 14

The week in stats (April 28th edition)

Two pieces of interesting data visualization work attracted some attention this week. How Americans Die by Matthew Klein of Bloomberg Visual Data and The Music America’s Listening To by Chris Kolmar of Movoto Blog.
Popular R articles of the week are: Testing for Linear Separability with Linear Programming in R by Raffael Vogler, Twitter Extraction by Ethan Fosse, Simpson’s Paradox Is Back by Mad (Data) Scientist, and Object Oriented Programming with R: An example with a Cournot duopoly by Bruno Rodrigues.
Have you ever tried Julia or have considered adopting it? Econometrics by Simulation reviews Julia from an R user’s perspective for those who are interested in learning this programming language.
Rapport summarizes some key metrics about the popularity of R like the number of R Foundation members per country all over the world, and presents his findings in a report called R activity around the world.
And finally, Why are R users so damn Stingy?!

Uncategorized — Comments Off
21
Apr 14

The week in stats (April 21st edition)

This is a Hilbert Cube, also named after David Hilbert.

Do you know anything about the Hilbert Matrix (other than it is probably named after David Hilbert)? In his post this week, Nicholas Horton, Professor of Statistics at Amherst College, explains what it is, and how to create these matrices using both SAS and R.
Xi’an discusses a new paper by Randal Douc, Florian Maire, and Jimmy Olsson called MCMC for sampling from mixture models.
Some popular statistical articles this week are: Modeling Data With Functional Programming In R by Cartesian Faith, Make your ggplots shareable, collaborative, and with D3 by Matt Sundquist, Implementing a Principal Component Analysis (PCA) by Sebastian Raschka (for Python), and Ordering Datasets Alphabetically by geomorph.
And finally, have you ever tried the popular mobile game 2048? If not, here are some code that you can run on your machine and start playing the game with R.

Uncategorized — 3 comments
14
Apr 14

The week in stats (April 14th edition)

R 3.1.0 (codename “Spring Dance“) is released this week!
Do you invest in the stock market? If so, you may know the so-called 60/40 rule (invest 40% in bonds and 60% in stocks). But do you really believe this strategy? Eran Raviv performs some simulation studies and tries to verify whether the 60/40 rule is a wise choice or simply a myth.
Popular R articles of the week: “Pretty” table columns and Calculating confidence intervals for proportions by Alan Haynes (Insights of a PhD student), Interpreting interaction coefficient in R by Lionel H. (biologyforfun) and Extract CSV data from PDF files with Tabula by Nathan Yau (Flowingdata).
And finally, the most loyal fans in the NBA are…

Uncategorized — Comments Off
07
Apr 14

The week in stats (April 7th edition)

To give this year’s April Fools’ day a more analytical touch, here are The 7 Funniest Data Cartoons.
Xi’an discusses a new paper by Scott Schmidler and his Ph.D. student Douglas VanDerwerken called Parallel MCMC.
Tim Harford of Financial Times shares his thoughts on Big Data in an article called Big data: are we making a big mistake?
David Springate publishes three very useful R articles this week: Develop in RStudio, run in RScript, Functional programming in R, and Two R tutorials for beginners.
And finally, Revolution Analytics summarizes some recent news and reports on how the rise of the “R” computer language brings open source to science.

Uncategorized — Comments Off
31
Mar 14

The week in stats (Mar. 31st edition)

Are you a fan of Wes Anderson? Revoluntion Analytics shares some ideas on how you can bring his style to your own R charts, by making use of these Wes Anderson inspired palettes.
Given 3 random variables X, Y and Z with known distributions, can you calculate cov(X, Y) from cov(X, Z) and cov(Y, Z)?
Some useful R tips this week are: Filtering Data with L1 Regularisation, quickly calculating summary statistics from a data frame, A Simple Introduction to the Graphing Philosophy of ggplot2, and Visualizing principal components with R and Sochi Olympic Athletes.
Xi’an reviews Bayesian Data Analysis by Andrew Gelman, John Carlin, Hal Stern, David Dunson, Aki Vehtari, and Don Rubin.
And finally, Nathan Yau of FlowingData presents some visuals from a study on smoking prevalence from 1996 to 2012, and concludes that smoking rate is inversely proportional to income level.

Uncategorized — Comments Off
24
Mar 14

The week in stats (Mar. 24th edition)

The German “Tank” Problem

James Paul Peruvankal of Revoluntion Analytics shares the secrets of teaching R. Joseph Rickert of the same organization publishes some online sources to download data sets in his article called Data Sets for Data Science.
Some interesting R related articles this week are: Species occurrence data by Karthik Ram of rOpenSci, barplot with ggplot2 by Martin Johnsson (PhD student at Linköping University), Stop using bivariate correlations for variable selection and The German Tank Problem: The Frequentist Way by Jacob Simmering (PhD student at University of Iowa), MCMC for Econometrics Students by Professor David Giles of University of Victoria (part I, part II and part III), Normality and Testing for Normality by Thomas Hopper (aka Learning as You Go), and It is time for RData files to become the standard for Data Transfer by Francis Smart (PhD student at Michigan State University).
Xi’an discusses his new paper (with Matthew Moores and Kerrie Mengersen) called Pre-processing for approximate Bayesian computation in image analysis.
And finally, the Royal Statistical Society publishes the Timeline of Statistics – a timeline with illustrations and texts that covers major events in the world of statistics starting from 450 BC.

Uncategorized — Comments Off
17
Mar 14

The week in stats (Mar. 17th edition)

R 3.0.3 is release (with installation and upgrading instructions and a list of updates, bug fixes and changes).
Suppose a company has 5 servers, and there is a 1% chance that each server will be down. What is the probability that at least 3 servers are down?
Mikio L. Braun, a PostDoc in machine learning at TU Berlin and co-founder and chief data scientist at streamdrill, discusses the difficulties of data analysis.
Xi’an comments on a new paper by his PhD student called Approximate Integrated Likelihood via ABC methods.
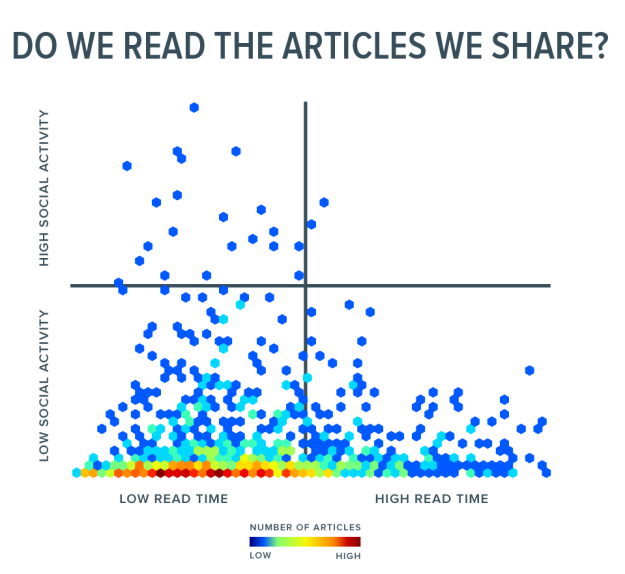
How people really read and share online.
Joseph Rickert of Revolution Analytics publishes his R “meta” book, a collection of 14 books (all available online for free) that covers useful topics including basic probability and statistics, regressions, experimental design, survival analysis, times series analysis and forecasting, machine learning, bioinformatics, structural equation models and credit scoring.
And finally, Flavio Barros compiles a list of MOOC courses on R.

Uncategorized — Comments Off
10
Mar 14

The week in stats (Mar. 10th edition)

A historian, a data scientist, a programmer, a mathematician, and a philosopher discuss the question How likely it is that a lottery draw (6 out of 49) contains two consecutive numbers.
Suppose that A, B, and C are uniformly distributed on [0, 1], what is the probability that the equation [latex] Ax^2 + Bx + C [/latex] has real root(s)?
Dimiter Toshkov of Rules of Reason presents Predicting movie ratings with IMDb data and R and suggests a different way of awarding the Academy Awards based on statistics.
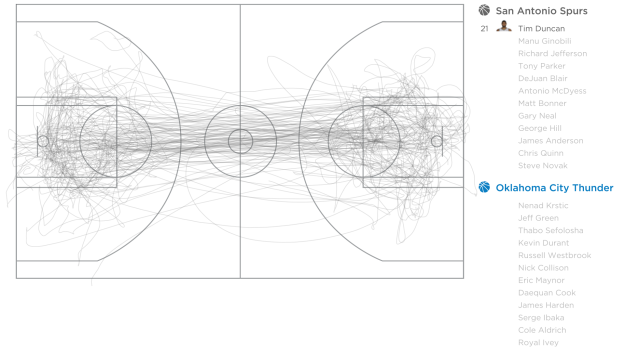
Visualized related articles are always liked by our readers. This week, we have: Plotting an Odd number of plots in single image, Beautiful table outputs in R, Visualizations on the Monopoly board, and Basketball movements visualized.
Xi’an reviews Bayesian Programming by Pierre Bessière, Emmanuel Mazer, Juan-Manuel Ahuactzin, and Kamel Mekhnacha.
Ever wonder how popular your favorite R functions are? Check out the Function Counter for R.
And finally, Rasmus Bååth shares easy ways to create matrices in R.

Uncategorized — 1 comment
03
Mar 14

The week in stats (Mar. 3rd edition)

Like almost every week, R articles attract lots of attention from readers. This week, we have: Quick and dirty notes on General Linear Mix Models, How to Make a Bad Password with R, rMaps and the Mexico map, How to Read Histograms and Use Them in R, Useful Functions in R for Manipulating Text Data, and Simply creating various scatter plots with ggplot.
r4stats.com publishes a detailed report on various ways of measuring the popularity or market shares of approximately 30 software packages for analytics, including well-known names such as R, Matlab, SAS, SPSS, Stata, Python.
Quintuitive discusses his experience and thoughts after using RStudio for one year.
Xi’an reviews two new books this week, the first one is called Nonlinear Time Series by Randal Douc, Éric Moulines and David Stoffer, and the second is called Foundations of Statistical Algorithms by Claus Weihs, Olav Mersman and Uwe Ligges.
If you are an active stock investor, you should consider Using CART for Stock Market Forecasting.
And finally, Nathan Yau of FlowingData explains the statistical reasoning behind why you should buy the bigger pizza.

News / Uncategorized — Comments Off
24
Feb 14

The week in stats (Feb. 24th edition)

The Mollusc Shell, created by the R function surf3D.

Last Monday (Feb. 17th) was R.A. Fisher’s birthday. To honor him, Deborah G. Mayo, Professor of Philosophy at Virginia Tech, publishes Fisher and Neyman after anger management, and R.A. Fisher: ‘Two New Properties of Mathematical Likelihood’.
A few articles related to visualization and graphics received lots of attention: ggplot2: Cheatsheet for Visualizing Distributions, Automatically coloring your R output in the terminal using colorout, A visual explanation of conditional probability, R: Fun with surf3D function and No need for SPSS – beautiful output in R.
Given that you have a five-card hand with ♠K and ♡K, what is the probability that you have all four Kings?
Coursera offers a new MOOC course called Data Analysis for Genomics. The course starts on April 7, 2014.
And finally, Arthur Charpentier (aka Freakonometrics) publishes a technical article called Identification of ARMA processes.

Probability and statistics blog

The week in stats (April 28th edition)

The week in stats (April 21st edition)

The week in stats (April 14th edition)

The week in stats (April 7th edition)

The week in stats (Mar. 31st edition)

The week in stats (Mar. 24th edition)

The week in stats (Mar. 17th edition)

The week in stats (Mar. 10th edition)

The week in stats (Mar. 3rd edition)

The week in stats (Feb. 24th edition)

Recent Posts

Recent Comments

Archives

Categories

Meta