“So let’s start with the fact that the study had only 100 people, which isn’t nearly enough to be able to make any determinations like this. That’s very small power. Secondly, it was already split into two groups, and the two groups by the way have absolutely zero scientific basis. There is no theory that says that if I want a girl or if I want a boy I’m going to be better able at determining whether my baby is in fact a girl or a boy.”
– Maria Konnikova, speaking on Mike Pesca’s podcast, The Gist.
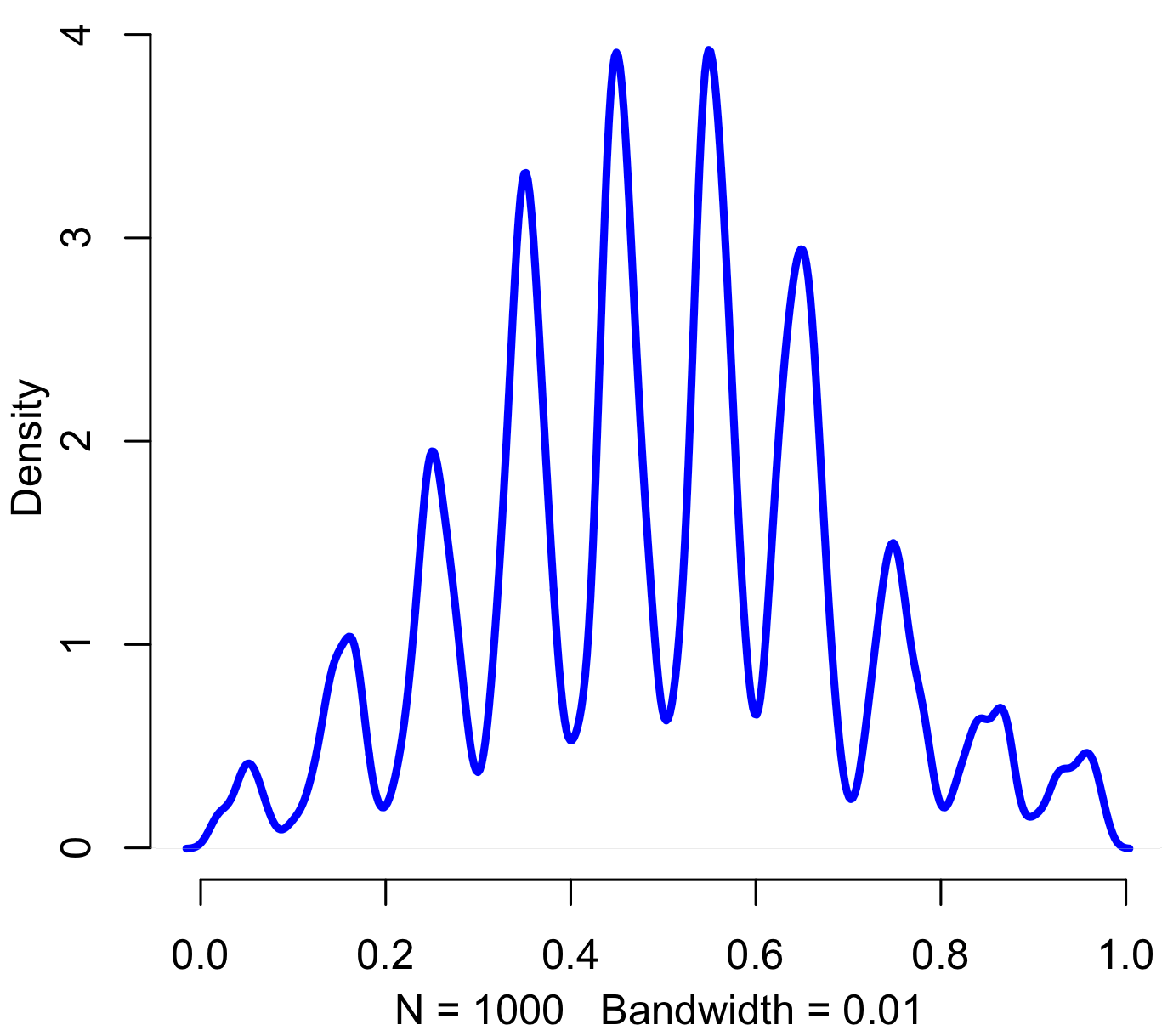
Shown at top, above the quote by Konnikova, is a simulation of the study in question, under the assumption that the results were completely random (the null hypothesis). As usual, you’ll find my code in R at the bottom. The actual group of interest had just 48 women. Of those, 34 correctly guessed the sex of their gestating babies. The probability that you’d get such an extreme result by chance alone is represented by the light green tails. To be conservative, I’m making this a two-tailed test, and considering the areas of interest to be either that the women were very right, or very wrong.
The “power” Konnikova is referring to is the “power of the test.” Detecting small effects requires a large sample, detecting larger effects can be done with a much smaller sample. In general, the larger your sample size, the more power you have. If you want to understand the relationship between power and effect size, I’d recommend this lovely video on the power of the test.
As it turns out, Konnikova’s claims notwithstanding, study authors Victor Shamas and Amanda Dawson had plenty of power to detect what turns out to be a very large effect. Adding together the two green areas in the tails, their study has a p-value of about 0.005. This a full order of magnitude beyond the generally used threshold for statistical significance. Their study found strong evidence that women can guess the sex of their babies-to-be.
Is this finding really as strong as it seems? Perhaps the authors made some mistake in how they setup the experiment, or in how they analyzed the results.
Since apparently Konnikova failed not only to do statistical analysis, but also basic journalism, I decided to clean up on that front as well. I emailed Dr. Victor Shamas to ask how the study was performed. Taking his description at face value, it appears that the particular split of women into categories was based into the study design; this wasn’t a case of “p-value hacking”, as Konnikova claimed later on in the podcast.
Konnikova misses the entire point of this spit, which she says has “absolutely zero scientific basis.” The lack of an existing scientific framework to assimilate the results of the study is meaningless, since the point of the study was to provide evidence (or not) that that our scientific understanding lags behind what woman seem to intuitively know.
More broadly, the existence of causal relationships does not depend in any way on our ability to understand or describe (model) them, or on whether we happen to have an existing scientific framework to fit them in. I used to see this kind of insistence on having a known mechanism as a dumb argument made by smart people, but I’m coming to see it in a much darker light. The more I learn about the history of science, the more clear it becomes that the primary impediment to the advancement of science isn’t the existence of rubes, it’s the supposedly smart, putatively scientific people who are unwilling to consider evidence that contradicts their worldview, their authority, or their self-image. We see this pattern over and over, perhaps most tragically in the unwillingness of doctors to wash their hands until germ theory was developed, despite evidence that hand washing led to a massive reduction in patient mortality when assisting with births or performing operations.
Despite the strength of Shamas and Dawson’s findings, I wouldn’t view their study as conclusive evidence of the ability to “intuit” the sex of your baby. Perhaps their findings were a fluke, perhaps some hidden factor corrupted the results (did the women get secret ultrasounds on the sly?). Like any reasonable scientist, Shamas wants to do another study to replicate the findings, and told me that has a specific follow-up in mind.
Code in R:
trials = 100000
results = rep(0,trials)
for(i in 1:trials) {
results[i] = sum(sample(c(0,1),48,replace=T))
}
extremes = length(results[results<=14]) + length(results[results>=34])
extremes/trials
dat <- data.frame( x=results, above=((results <= 14) | (results >= 34)))
library(ggplot2)
qplot(x,data=dat,geom="histogram",fill=above,breaks=seq(1,48))